📌 본 포스팅은 통계교육원(https://sti.kostat.go.kr/)
이러닝 교육과정 '통계학의 이해(2023)' 강의에 대한 복습 기록입니다.
모든 내용은 강의 교안을 기준으로 작성했으며 원본 자료는 하단 통계교육원 - 교육과정 - 이러닝 - '통계학의 이해' 교육 수강을 통해 무료로 열람 가능하고 교육자료는 저작권자의 동의 없이 무단 복제 및 배포할 수 없습니다.
🎯
신뢰구간의 기본 개념 알기
모평균의 신뢰구간
구하는 방법
💡
1. 신뢰구간의 기본 개념
2. 모평균에 대한 신뢰구간
📖 신뢰구간, 신뢰수준, 오차한계, 표준오차, t분포
1. 신뢰구간의 기본 개념
# 구간추정
관심 있는 미지의 모수(θ)가 있을 때, 미지의 모수(θ)가 속할 것이라고 기대되는 구간을 제시하여 추정하는 것
이러한 구간을 '신뢰구간'이라고 한다.
# 신뢰구간
관심 있는 모수를 θ라 할 때 두 통계량 L과 U가 있어서
P ( L < θ < U ) = 1 - α
를 만족할 때 구간 ( L, U)을 θ에 대한 100(1 - α) % 신뢰구간이라 한다.
· L을 신뢰하한 (confidence lower limit)
· R을 신뢰상한 (confidence upper limit)
· (1 - α) = 신뢰수준(Confidence level)
# 신뢰수준
은 일반적으로 α가 0.1, 0.05, 0.01이 되는 90% 95% 99% 를 주로 사용한다.
✔ 신뢰구간에서 신뢰수준 95%라는 의미는? 🤔
→ 모수 θ를 갖는 모집단으로부터 같은 크기의 랜덤 표본을 여러개 추출했을 때
각각의 표본으로부터 얻은 신뢰구간중 95% (α = 0.05) 에 해당하는 구간이 모수 θ를 포함하고
나머지는 포함하지 않는다는 의미이다.

위 그림과 같이 크기가 같은 100개의 랜덤 표본으로부터 신뢰구간을 구하면
100개 중 대략 95개는 모수의 참값을 포함한다는 것!
2. 모평균에 관한 신뢰구간
평균이 μ 이고 분산이 σ² 인 모집단에서
크기가 n 인 랜덤표본 X₁ ... Xn 을 추출하여 모평균 μ 의 신뢰구간을 구하는 방법
2-1. 모집단의 분포가 정규분포를 따를 때 (모분산 σ²을 알 때)
모집단의 분표가 정규분포를 따르면
정규분포 성질에 의해 표본평균도 다음과 같은 정규분포를 따른다.

따라서 다음과 같이 표준화된 확률번수는 표준정규분포를 따른다.


즉 표준정규분포의 분위수 개념을 이용하면

이 성립한다.
이 식을 모평균 μ 에 대해 정리하면

를 만족하는 식을 얻을 수 있다.
신뢰구간의 정의에 의해 μ 에 대한 100(1-α) % 신뢰구간은

가 된다.
여기서 신뢰하한, 신뢰상한, 오차한계(Limit of error)를 구하면
| 신뢰하한 | 신뢰상한 | 오차한계 |
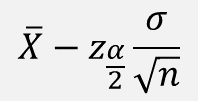 |
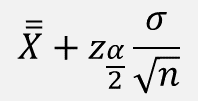 |
 |
신뢰구간의 길이 = 신뢰상한 - 신뢰하한
| 신뢰구간 길이 |
 |
즉, 신뢰하한(/상한)은 모평균 μ 의 점추정치 X ̅ 에
오차 한계(꼬리 확률이 α/2 에 해당하는 분위수 Z α/2 와 표준오차 α / √n 의 곱)의 차이에 의해 구할 수 있다.
신뢰구간의 길이를 생각했을 때
똑같은 신뢰수준이라면 신뢰구간이 짧은 것이 좋다는 것을 알 수 있다.
- 모집단의 표준편차 σ 가 작으면 작아지고
- 표본 크기 n이 커지면 작아진다.
2-2. 모집단의 분포가 정규분포를 따를 때 (모분산 σ²을 모를 때)
모집단이 정규분포를 따를 때 신뢰구간은 아래와 같았다.

그러나 이 신뢰구간은 모집단의 표준편차 σ를 모르면 사용할 수 없다.
실제 문제에서 모분산은 알지만 모평균을 모르는 경우는 현실적으로 많지 않고
두 모수 모두 모르는 경우가 대부분이다.
모분산을 모르는 경우에는
σ 대신 σ의 추정량인 표본분산 S를 대입해서 사용해야 한다.
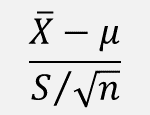 |
 |
그러나 위 통계량은 표준정규분포를 따르지 않는다.
다행히 위 통계량은 자유도가 (n-1)인 t분포를 따른다는 사실이 알려져 있다.
# t 분포
t분포는 X₁ X₂ X₃ X₄ ... X n를 N( μ , σ²) 으로부터 랜덤 표본이라 할 때
확률변수 T를 아래와 같이 정의하면

T는 자유도(degree of freedom, df)가 (n-1)인 t-분포를 따르고
이를 T ~ t (n-1)로 표현한다.
# t분포의 모양

표준정규분포와 t분포를 비교한 그림
t분포가 표준 정규분포보다 꼬리 부분 확률이 조금 더 크다.
- t분포 모양은 표준정규분포와 유사하게 종모양을 이루고 0을 중심으로 대칭이다.
· 차이점
- 평균과 멀리 떨어진 꼬리 근처의 밀도가 정규분포보다 높다.
t분포를 따르는 자료는 평균과 멀리 떨어진 자료(이상치)들이 표준정규분포에 비해 많다는 것을 의미한다.
t분포는 자유도(n-1) 즉 표본의 크기가 커지면 정규분포와 비슷한 모양을 지니게 된다.
표본이 크면 S²이 σ²과 매우 비슷해질 것이기 때문!
∴ 정규분포인 모집단에서 표본 크기가 작고, 모분산을 모를 경우 신뢰구간은 위에서 설명한 t분포에 의해 구할 수 있다.

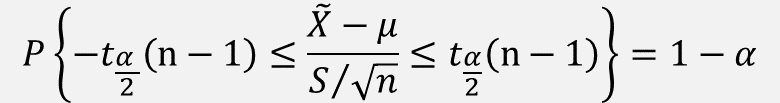
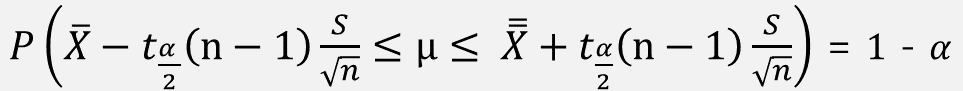
∴ μ 의 100(1-σ) % 신뢰구간은
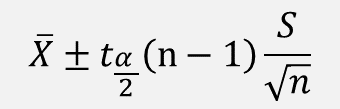
여기서 t α/2 (n-1) 은 Z α/2 와 유사하게 자유도가 (n-1)인 t분포에서 꼬리확률이 α/2 에 해당하는 분위수를 의미한다.
'기초통계' 카테고리의 다른 글
| [통계학의 이해] 17. 가설검정의 원리 (0) | 2023.09.30 |
|---|---|
| [통계학의 이해] 16. 신뢰구간의 이해 -2 (0) | 2023.09.26 |
| [통계학의 이해] 14. 통계적 추정 (0) | 2023.09.23 |
| [통계학의 이해] 13. 표본 분포의 이해 (0) | 2023.09.23 |
| 예제를 활용한 가설검정과 분석도구 (0) | 2023.09.04 |