상호작용과 인과 : 상호작용
상호작용 Interaction
두 독립변수의 곱으로 이뤄진 항(xm)

• 관계식으로 쓸 때는 : 을 사용
y ~ x + m + x:m
• 관계식에서 x*m 은 x+m + x:m 과 같음. (즉 더하기랑 곱하기를 다 해라)
예 시
• x 는 연속형
• m 은 0 또는 1만 갖는 범주형 변수 (설명의 편의를 위한 단순화)
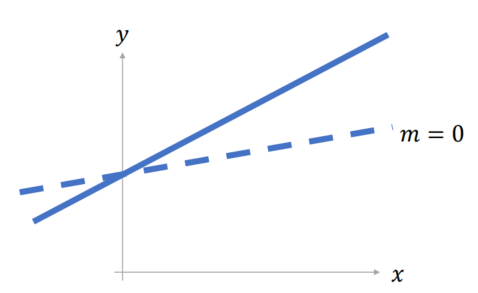
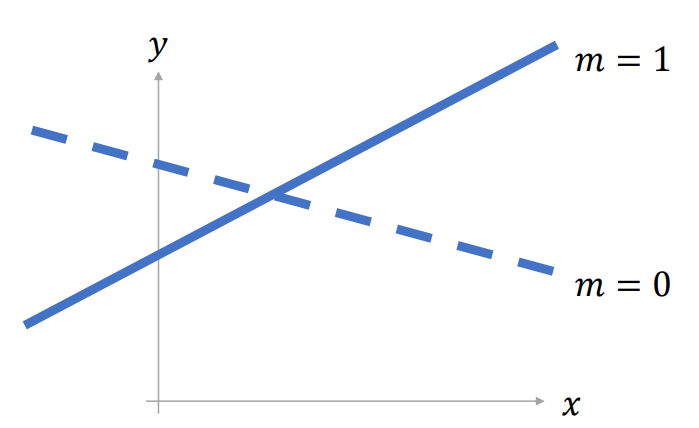
| > 상호작용이 없는 경우 | > 기울기가 달라지는 경우 | > 기울기와 절편 모두 달라지는 경우 |
| 수식형태로 쓰면 y = ax + bm + c |
계수를 포함해서 수식 형태로 쓰면 y = ax + bxm + c |
계수를 포함해서 수식 형태로 쓰면 y = ax + bm + cxm + d |
| • m에 따라 x의 절편이 바뀌는 것으로 해석 | • m에 따라 x의 기울기가 바뀌는 것으로 해석 | • m에 따라 x의 절편과 기울기가 바뀌는 것으로 해석 |
 |
 |
 |
| m=1, y = ax + (b + c) m=0, y = ax + c > 기울기는 똑같이 a고 절편이 다름. |
m=1, y = (a+b)x + c m=0, y = ax + c > 기울기가 다르고 절편이 같음. |
m=1, y=(a+c) x + (b+d) m=0, y = ax + d > 절편은 b만큼 차이나고 기울기는 c만큼 차이가 난다. |
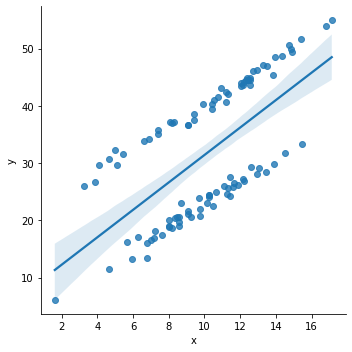
Python에서의 절편의 차이
import pandas as pd
df1 = pd.read_excel("diff_intercept.xlsx")
df1.head()
import seaborn as sns
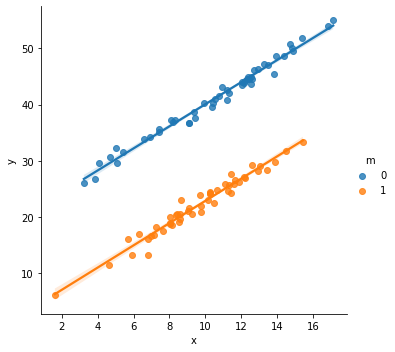
sns.scatterplot(x='x',y='y', hue='m', data=df1)
| import seaborn as sns sns.lmplot(x='x', y='y', data=df1) |
import seaborn as sns sns.lmplot(x='x', y='y', hue='m', data=df1) # 그룹 m을 따로 그릴경우 |
 |
 |
| from statsmodels.formula.api import ols ols('y ~ x', df1).fit().summary() |
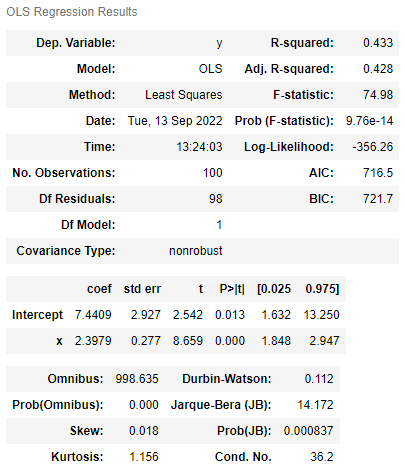
from statsmodels.formula.api import ols ols('y ~ x + m', df1).fit().summary() |
 |
 |
x=0, y =2.3979 |
y = 20.3857 + 1.9659 x - 17.1611m m = 0, y = 20.3857 + 1.9659 x m = 1, y = 20.3857 + 1.9659 x - 17.1611 x = 0, y = -17.1661 > 즉 여기서 나타내는 -17.1661은 절편의 차이 |
Q. 두 직선이 기울기가 같은지 다른지 어떻게 아는가?
귀무가설 : m의 계수가 0이다 > 절편에 차이가 없다.
m의 p-val < 0.05이다. > 귀무가설 기각
∴ 기울기가 차이가 있다.
| from statsmodels.formula.api import ols ols('y ~ x + x:m', df1).fit().summary() |
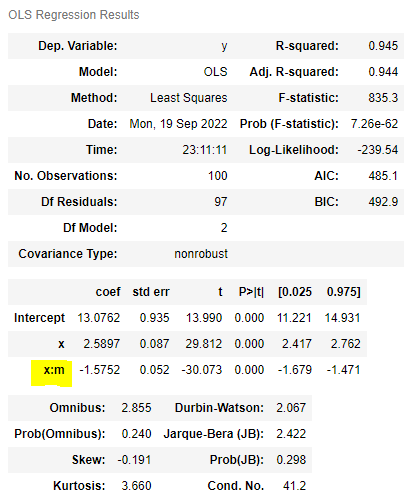
from statsmodels.formula.api import ols ols('y ~ x + m + x:m', df1).fit().summary() |
 |
 |
| > '절편이 다르다'는 귀무가설 기각 '기울기가 다르다'는 귀무가설 기각X 즉 기울기가 같다. |
|
| y = 13.0762 + 2.5897 x - 1.5752 xm m = 0, y = 13.0762 + 2.5897 x m = 1, y = 13.0762 + (2.5897 - 1.5752) x 즉, x:m의 계수는 두 직선의 기울기의 차이 |
1) 모형과 모형을 비교
y ~ x + m 과 y ~ x + m + x:m의 회귀분석 결과를 비교해보면,
기울기가 같다고 가정한 모형이 기울기가 다르다고 가정한 모형보다 수정R계수, AIC, BIC가 모두 더 좋다.
> 즉 기울기가 같다고 주장할 수 있다.
2) '기울기와 절편이 다르다'는 모형으로 분석
'y ~ x + m'과 'y ~ x + m + x:m' 각각의 계수로 통계적 가설 검정
기울기가 같다는 귀무가설을 기각 X → '기울기가 같다'고 주장할 수 있다.
● m의 계수를 보는 경우
예1) 통계 공부를 한다.
기울기가 다르다. = 시간 대비 늘어나는 지식
'oo에게 배우면 혼자 공부하는 것보다 훨씬 빠르게 공부할 수 있다' (=기울기가 다르다고 주장하는 것)
위의 주장에 반박하려면 기울기를 확인해보면 된다.
예2) 다이어트 약품
' A사 다이어트 약품을 먹고 밥을 안먹으면 살이 쭉쭉 빠져요.'
의문> 밥을 안먹으면 살이 원래 빠지는 것 아닌가?
● 절편, 기울기가 다른 경우를 설명하는 예시 Data : birthsmokers
 |
 |
 |
| m = 1 (비흡연) m = 0 (흡연) > 몸무게는 주수가 길어질수록 늘어나는데 임산부가 흡연자인 경우와 비흡연자인 경우에 따라 일정한 무게차이가 계속 지속됨. |
m = 1(비흡연) m = 0(흡연) > 몸무게가 늘어나긴 늘어나는데 엄마가 비흡연자인 경우 몸무게가 빠르게 증가하고 흡연자인 경우 몸무게 증가가 더딜 가능성도 있다. |
* 그래프에 대한 설명은 사실이 아니며, 단순 그래프 설명을 위한 예시이다.
Q. 두모형 중에 독립변수와 상호작용항만 넣은 모형(y = x + x*m) 보다 통제변수항과 상호작용항을 동시에 넣고 보는 모형 (y = x + m + x*m)이 더 많이 보았는데 y = x + x*m도 많이 쓰이는지?
> 분석에 가설에 따라서 다르다.
y = x + x*m: 실제로는 절편이 다른 경우에도 기울기의 차이가 유의하게 나올 수 있다.
'기초통계' 카테고리의 다른 글
| 상호작용과 인과 : 횡단 비교와 종단 비교 (0) | 2022.09.13 |
|---|---|
| 상호작용과 인과 : 인과효과 (0) | 2022.09.13 |
| 로지스틱회귀분석 : 혼동행렬, ROC_Curve (0) | 2022.09.13 |
| [실습] 회귀분석 : birthsmokers data (0) | 2022.09.10 |
| 로지스틱 회귀분석 (0) | 2022.09.06 |


