횡단 비교와 종단 비교
KEYWORD
횡단비교와 종단비교
이중차분법
횡단비교 & 종단비교
• 횡단(cross-sectional) 비교: 동일 시점에 다른 대상이나 집단을 비교
• 종단(longitudinal) 비교: 동일 대상을 다른 시점 간 비교
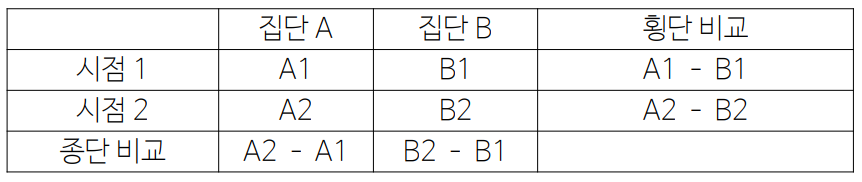
이중차분법 Difference-in-Differences
실험이 불가능한 상황에서 사용하는 준실험적 방법
• 실험군 A에 어떤 처치를 했으나 대조군 B가 없을 때
• A와 비슷한 집단 B를 이용하여 비교
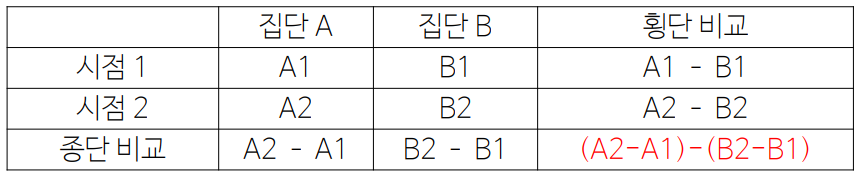
> 결과 해석
d = (A2 - A1) - (B2 - B1)
d = 0, 실험군 A에서 변화는 대조군 B에서의 변화와 비슷 → 처치 효과 X
d ≠ 0, 실험군 A에서 대조군 B와 다른 변화를 관찰 → 처치 효과 O
평행 추세의 가정 parallel trend assumption
처치 효과가 없다면, 실험군 A와 실험군 B가 비슷하게 변할 것이라고 가정
• 이러한 가정이 성립하지 않는다면 이중차분법의 결과는 무의미
• 가능한 비슷한 A와 B를 비교하는 것이 중요
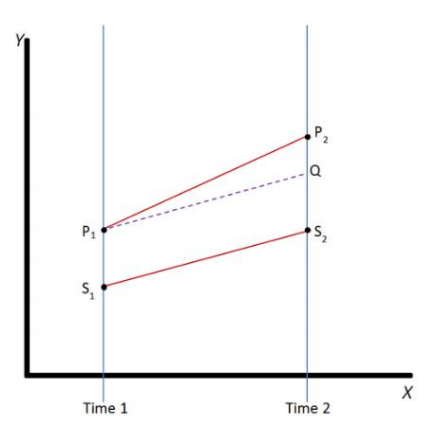
회귀분석을 통한 이중차분법
- 상호작용을 이용해 분석
𝑦 = 𝑎 ∙ GROUP + 𝑏 ∙ POINT + 𝑑 ∙ ( GROUP × POINT ) + 𝑒
• GROUP : 집단 A(1), 집단 B(0)
• POINT : 처치 전(0), 처치 후(1)
• a = 처치 전 두 집단의 차이
• b = 대조군(B)의 전후 차이
• d = 전후에 B보다 A의 변화가 얼마나 큰지
(시점1) => point(0)
(시점2) => point(1)
기울기의 해석

예) 알러지 반응에 대한 프로폴리스 섭취 효과
| 집단 A (프로폴리스 섭취O) | 집단 B (프로폴리스 섭취X) | 횡단비교 | |
| 시점1 | 알레르기 수치 30점 | 알레르기 수치 50점 | 20점 |
| 시점2 | 알레르기 수치 20점 | 알레르기 수치 40점 | 20점 |
| 종단비교 | 10점 | 10점 | 0 |
> 프로폴리스를 먹은 집단 A와 프로폴리스를 먹지 않은 집단 B 모두 알레르기 수치가 10점씩 줄었다.
따라서 d가 0이므로 프로폴리스는 알러지 반응을 낮추는데 효과가 없다고 말할 수 있다.
> 이중차분법을 적용한 논문
Card & Krueger (1994)
최저임금의 상승이 고용에 미치는 효과를 측정
• 1992년 미국 뉴저지 주는 최저 임금을 시간당 4.25달러에서 5.05달러 로 인상
• 이웃 펜실베니아 주는 4.25달러 최저 임금을 유지
> 두 주 경계에 위치한 패스트푸드 음식점을 대상으로 고용 변화를 조사
import pandas as pd
nm3 = pd.read_excel('njmin3.xlsx')
nm3.head()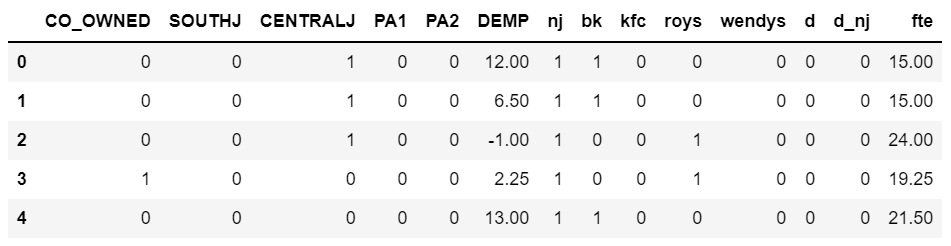
· fte = full time employment : 고용률 > y
· nj : 0=펜실베니아 1=뉴저지
· d :0=최저임금 인상 전 1=후
from statsmodels.formula.api import ols
ols('fte ~ nj + d + nj:d', nm3).fit().summary()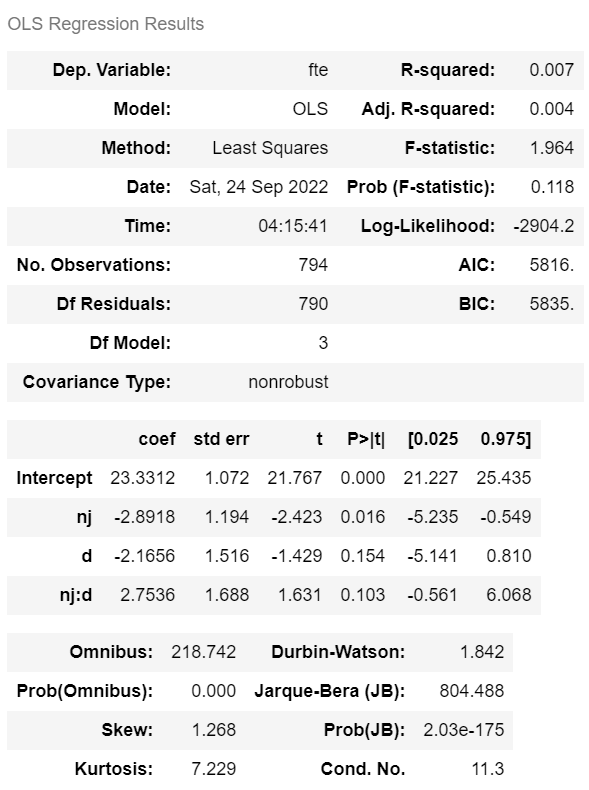
y = -2.8918 nj -2.1656 d + 2.7536 ( nj × d ) + 23.3312
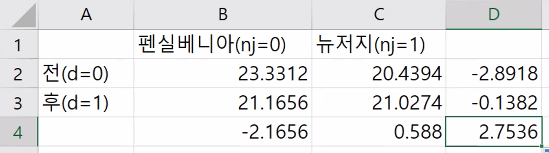
결과해석
> d (2.7536) ← 최저임금 인상의 효과
최저 임금을 올렸는데 고용이 늘어난다?
No!
p-val = 0.103으로 0.005보다 크므로 귀무가설을 기각하지 못하고 통계적으로 유의미한 의미가 없다.
즉, 최저임금을 올려서 고용이 늘었다고도 줄었다고도 할 수 없다.
한계점
대기업은 최저임금 변화에 따라 대응하는 방식이 다양하고, 최저임금이 오른다고 바로 해고하지도 않는다.
연습
"광고를 한 그룹에서 광고 전 / 후의 매출 차이를 이중 차분법으로 분석해보자"
> 데이터 import
import pandas as pd
pa = pd.read_excel('postAd.xlsx')
pa.head()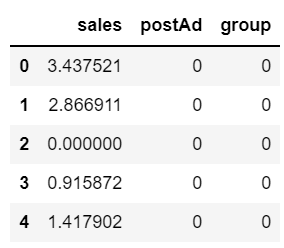
· postAd : 광고 전(0), 광고 후(1)
· group : 광고 안한 그룹(0), 광고 한 그룹(1)
· sales : 매출
> 회귀분석 : 상호작용 적용
from statsmodels.formula.api import ols
ols('sales ~ postAd + group + postAd:group', pa).fit().summary()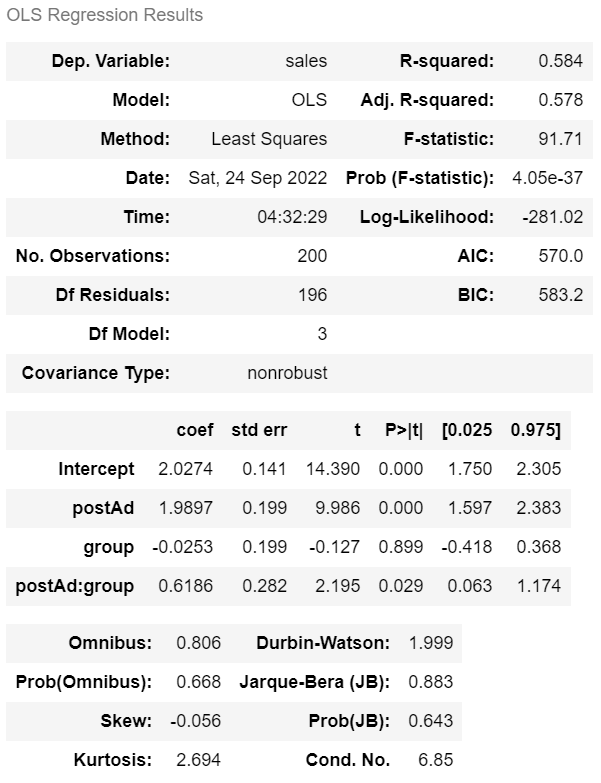
y = 1.9897 x postAd - 0.0253 x group + 0.6186 (postAd x group) + 2.0274
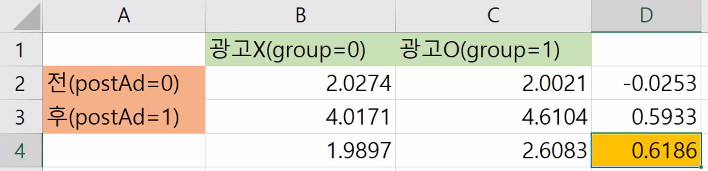
결과해석
> 광고효과가 0.6186 만큼 발생하였는데
p-val = 0.025 로 <0.05로 통계적으로 유의미하므로
광고 효과가 있다고 할 수 있다.
'기초통계' 카테고리의 다른 글
| [차원축소와 군집분석] 군집분석 : Clustering (0) | 2022.10.04 |
|---|---|
| [기초통계] 차원 축소와 군집 분석 (0) | 2022.09.15 |
| 상호작용과 인과 : 인과효과 (0) | 2022.09.13 |
| 상호작용과 인과 : 상호작용 (0) | 2022.09.13 |
| 로지스틱회귀분석 : 혼동행렬, ROC_Curve (0) | 2022.09.13 |