차원 축소와 군집 분석
비지도 학습 unsupervised learning
주어진 데이터의 내재적 구조를 분석
지도학습과 달리 데이터 자체에 정답이 없음
• 종류:
- 차원 축소 dimensionality reduction (점수만들기)
- 군집 분석 clustering (비슷한 것끼리 모으기)
차원 축소 Dimensionality Reduction
데이터에서 차원 = 변수의 수
차원이 크면 ?
• 시각화가 어려움 (대부분 시각화는 2차원)
• 이해하기 어려움 (사람이 생각할 수 있는 차원에는 한계)
• 분석하기 어려움 (차원이 클수록 과적합이 일어나기 쉬움)
> 변수가 늘어난다 = 차원이 늘어난다.
(수정 R제곱, AIC, BIC는 이런 것을 보정해준다.)
• 차원 축소: 차원을 줄이는 다양한 기법들
차원 축소로서 평균점수
여러 과목의 점수를 평균 내어 점수내는 것도 일종의 차원 축소
• 과목이 많으면 → 점수가 많아짐 → 이해/비교하기 어려움
• 평균을 내면 → 점수가 하나로 줄어듦 → 이해/비교하기가 쉬움
• 가중치를 두기도 함 → 근거는???
합점수

각 행의 모든 값의 단순 합
> x.sum(axis=1)
Python에서 합점수
① Data import
데이터 출처 :
https://archive.ics.uci.edu/ml/datasets/iris
UCI Machine Learning Repository: Iris Data Set
Data Set Characteristics: Multivariate Number of Instances: 150 Area: Life Attribute Characteristics: Real Number of Attributes: 4 Date Donated 1988-07-01 Associated Tasks: Classification Missing Values? No Number of Web Hits: 4907053 Source: Creator:
archive.ics.uci.edu
import pandas as pd
iris = pd.read_excel('iris.xlsx')
# iris.head()
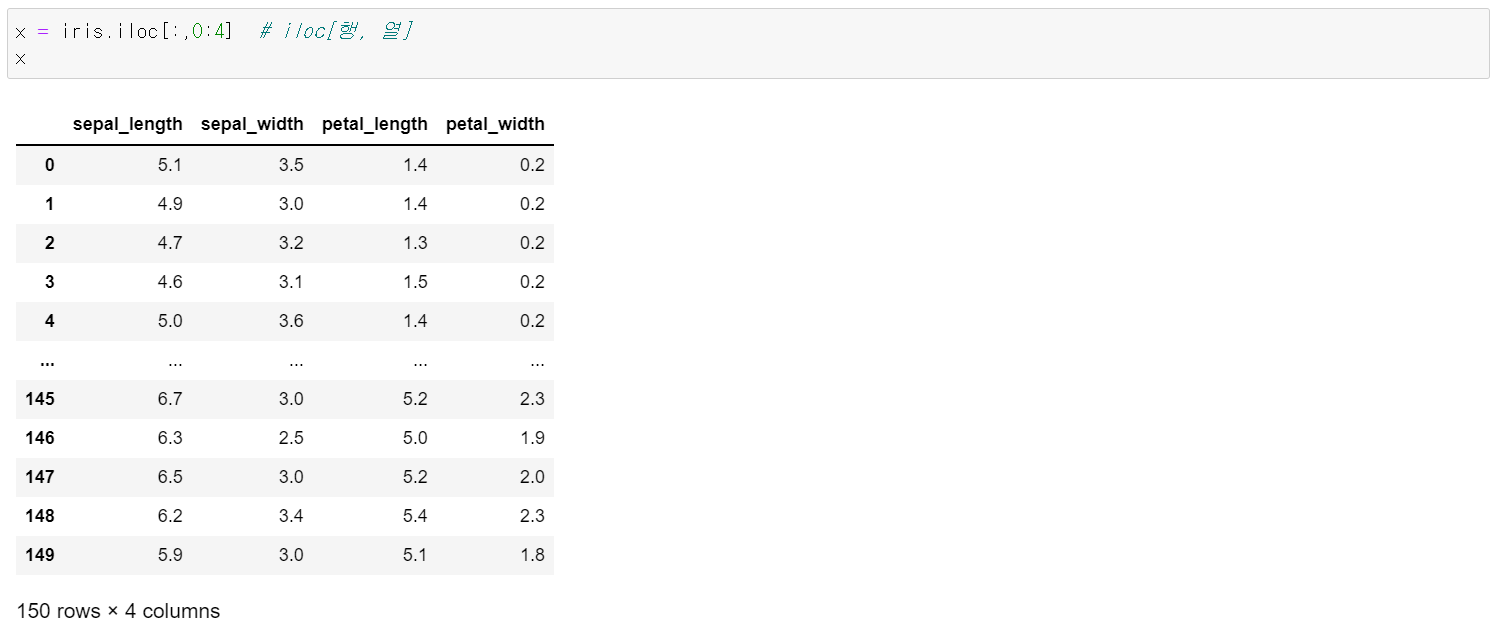
x = iris.iloc[:,0:4] # iloc[행, 열]
x
② 합점수
x.sum(axis=1)
• 변수마다 평균과 분산이 달라, 실질적인 반영 비율에 차이가 생긴다.
x.describe()
petal_length 는 min~ max 범위가 커서 총점에 반영이 크게 되지만
sepal_width 는 min~max 범위가 작아서 총점에 반영되는 부분이 적게 된다.
★ 이것을 극복하기 위한 것이 '표준화'
표준화 Standardization
모든 변수의 분포를 비슷하게 만들기 위한 절차
( X - 평균) / 표준편차
> 표준화하면 평균 0, 표준편차 1이 됨.
StandardScaler = ( X - 평균) / 표준편차 평균 0 표준편차1
MinMaxScaler = (X - 최소) / 범위 0 ~ 1
범주형 변수 여러개가 있으면 합해서 새로운 변수로 만들어준다.예) 자격증 A, B, C가 있다면 자격증 수
Python에서 표준화하기
from sklearn.preprocessing import StandardScaler
# StandardScaler
from sklearn.preprocessing import StandardScaler
std = StandardScaler()
# 데이터에 적합(평균과 표준편차를 구해서 저장)
std.fit(x)
# 변환
z = std.transform(x)
zz ▼
array([[-9.00681170e-01, 1.01900435e+00, -1.34022653e+00,
-1.31544430e+00],
[-1.14301691e+00, -1.31979479e-01, -1.34022653e+00,
-1.31544430e+00],
[-1.38535265e+00, 3.28414053e-01, -1.39706395e+00,
-1.31544430e+00],
[-1.50652052e+00, 9.82172869e-02, -1.28338910e+00,
-1.31544430e+00],
[-1.02184904e+00, 1.24920112e+00, -1.34022653e+00,
-1.31544430e+00],
[-5.37177559e-01, 1.93979142e+00, -1.16971425e+00,
-1.05217993e+00],
[-1.50652052e+00, 7.88807586e-01, -1.34022653e+00,
-1.18381211e+00],
[-1.02184904e+00, 7.88807586e-01, -1.28338910e+00,
-1.31544430e+00],
[-1.74885626e+00, -3.62176246e-01, -1.34022653e+00,
-1.31544430e+00],
[-1.14301691e+00, 9.82172869e-02, -1.28338910e+00,
-1.44707648e+00],
[-5.37177559e-01, 1.47939788e+00, -1.28338910e+00,
-1.31544430e+00],
[-1.26418478e+00, 7.88807586e-01, -1.22655167e+00,
-1.31544430e+00],
[-1.26418478e+00, -1.31979479e-01, -1.34022653e+00,
-1.44707648e+00],
[-1.87002413e+00, -1.31979479e-01, -1.51073881e+00,
-1.44707648e+00],
[-5.25060772e-02, 2.16998818e+00, -1.45390138e+00,
-1.31544430e+00],
[-1.73673948e-01, 3.09077525e+00, -1.28338910e+00,
-1.05217993e+00],
[-5.37177559e-01, 1.93979142e+00, -1.39706395e+00,
-1.05217993e+00],
[-9.00681170e-01, 1.01900435e+00, -1.34022653e+00,
-1.18381211e+00],
[-1.73673948e-01, 1.70959465e+00, -1.16971425e+00,
-1.18381211e+00],
[-9.00681170e-01, 1.70959465e+00, -1.28338910e+00,
-1.18381211e+00],
[-5.37177559e-01, 7.88807586e-01, -1.16971425e+00,
-1.31544430e+00],
[-9.00681170e-01, 1.47939788e+00, -1.28338910e+00,
-1.05217993e+00],
[-1.50652052e+00, 1.24920112e+00, -1.56757623e+00,
-1.31544430e+00],
[-9.00681170e-01, 5.58610819e-01, -1.16971425e+00,
-9.20547742e-01],
[-1.26418478e+00, 7.88807586e-01, -1.05603939e+00,
-1.31544430e+00],
[-1.02184904e+00, -1.31979479e-01, -1.22655167e+00,
-1.31544430e+00],
[-1.02184904e+00, 7.88807586e-01, -1.22655167e+00,
-1.05217993e+00],
[-7.79513300e-01, 1.01900435e+00, -1.28338910e+00,
-1.31544430e+00],
[-7.79513300e-01, 7.88807586e-01, -1.34022653e+00,
-1.31544430e+00],
[-1.38535265e+00, 3.28414053e-01, -1.22655167e+00,
-1.31544430e+00],
[-1.26418478e+00, 9.82172869e-02, -1.22655167e+00,
-1.31544430e+00],
[-5.37177559e-01, 7.88807586e-01, -1.28338910e+00,
-1.05217993e+00],
[-7.79513300e-01, 2.40018495e+00, -1.28338910e+00,
-1.44707648e+00],
[-4.16009689e-01, 2.63038172e+00, -1.34022653e+00,
-1.31544430e+00],
[-1.14301691e+00, 9.82172869e-02, -1.28338910e+00,
-1.31544430e+00],
[-1.02184904e+00, 3.28414053e-01, -1.45390138e+00,
-1.31544430e+00],
[-4.16009689e-01, 1.01900435e+00, -1.39706395e+00,
-1.31544430e+00],
[-1.14301691e+00, 1.24920112e+00, -1.34022653e+00,
-1.44707648e+00],
[-1.74885626e+00, -1.31979479e-01, -1.39706395e+00,
-1.31544430e+00],
[-9.00681170e-01, 7.88807586e-01, -1.28338910e+00,
-1.31544430e+00],
[-1.02184904e+00, 1.01900435e+00, -1.39706395e+00,
-1.18381211e+00],
[-1.62768839e+00, -1.74335684e+00, -1.39706395e+00,
-1.18381211e+00],
[-1.74885626e+00, 3.28414053e-01, -1.39706395e+00,
-1.31544430e+00],
[-1.02184904e+00, 1.01900435e+00, -1.22655167e+00,
-7.88915558e-01],
[-9.00681170e-01, 1.70959465e+00, -1.05603939e+00,
-1.05217993e+00],
[-1.26418478e+00, -1.31979479e-01, -1.34022653e+00,
-1.18381211e+00],
[-9.00681170e-01, 1.70959465e+00, -1.22655167e+00,
-1.31544430e+00],
[-1.50652052e+00, 3.28414053e-01, -1.34022653e+00,
-1.31544430e+00],
[-6.58345429e-01, 1.47939788e+00, -1.28338910e+00,
-1.31544430e+00],
[-1.02184904e+00, 5.58610819e-01, -1.34022653e+00,
-1.31544430e+00],
[ 1.40150837e+00, 3.28414053e-01, 5.35408562e-01,
2.64141916e-01],
[ 6.74501145e-01, 3.28414053e-01, 4.21733708e-01,
3.95774101e-01],
[ 1.28034050e+00, 9.82172869e-02, 6.49083415e-01,
3.95774101e-01],
[-4.16009689e-01, -1.74335684e+00, 1.37546573e-01,
1.32509732e-01],
[ 7.95669016e-01, -5.92373012e-01, 4.78571135e-01,
3.95774101e-01],
[-1.73673948e-01, -5.92373012e-01, 4.21733708e-01,
1.32509732e-01],
[ 5.53333275e-01, 5.58610819e-01, 5.35408562e-01,
5.27406285e-01],
[-1.14301691e+00, -1.51316008e+00, -2.60315415e-01,
-2.62386821e-01],
[ 9.16836886e-01, -3.62176246e-01, 4.78571135e-01,
1.32509732e-01],
[-7.79513300e-01, -8.22569778e-01, 8.07091462e-02,
2.64141916e-01],
[-1.02184904e+00, -2.43394714e+00, -1.46640561e-01,
-2.62386821e-01],
[ 6.86617933e-02, -1.31979479e-01, 2.51221427e-01,
3.95774101e-01],
[ 1.89829664e-01, -1.97355361e+00, 1.37546573e-01,
-2.62386821e-01],
[ 3.10997534e-01, -3.62176246e-01, 5.35408562e-01,
2.64141916e-01],
[-2.94841818e-01, -3.62176246e-01, -8.98031345e-02,
1.32509732e-01],
[ 1.03800476e+00, 9.82172869e-02, 3.64896281e-01,
2.64141916e-01],
[-2.94841818e-01, -1.31979479e-01, 4.21733708e-01,
3.95774101e-01],
[-5.25060772e-02, -8.22569778e-01, 1.94384000e-01,
-2.62386821e-01],
[ 4.32165405e-01, -1.97355361e+00, 4.21733708e-01,
3.95774101e-01],
[-2.94841818e-01, -1.28296331e+00, 8.07091462e-02,
-1.30754636e-01],
[ 6.86617933e-02, 3.28414053e-01, 5.92245988e-01,
7.90670654e-01],
[ 3.10997534e-01, -5.92373012e-01, 1.37546573e-01,
1.32509732e-01],
[ 5.53333275e-01, -1.28296331e+00, 6.49083415e-01,
3.95774101e-01],
[ 3.10997534e-01, -5.92373012e-01, 5.35408562e-01,
8.77547895e-04],
[ 6.74501145e-01, -3.62176246e-01, 3.08058854e-01,
1.32509732e-01],
[ 9.16836886e-01, -1.31979479e-01, 3.64896281e-01,
2.64141916e-01],
[ 1.15917263e+00, -5.92373012e-01, 5.92245988e-01,
2.64141916e-01],
[ 1.03800476e+00, -1.31979479e-01, 7.05920842e-01,
6.59038469e-01],
[ 1.89829664e-01, -3.62176246e-01, 4.21733708e-01,
3.95774101e-01],
[-1.73673948e-01, -1.05276654e+00, -1.46640561e-01,
-2.62386821e-01],
[-4.16009689e-01, -1.51316008e+00, 2.38717193e-02,
-1.30754636e-01],
[-4.16009689e-01, -1.51316008e+00, -3.29657076e-02,
-2.62386821e-01],
[-5.25060772e-02, -8.22569778e-01, 8.07091462e-02,
8.77547895e-04],
[ 1.89829664e-01, -8.22569778e-01, 7.62758269e-01,
5.27406285e-01],
[-5.37177559e-01, -1.31979479e-01, 4.21733708e-01,
3.95774101e-01],
[ 1.89829664e-01, 7.88807586e-01, 4.21733708e-01,
5.27406285e-01],
[ 1.03800476e+00, 9.82172869e-02, 5.35408562e-01,
3.95774101e-01],
[ 5.53333275e-01, -1.74335684e+00, 3.64896281e-01,
1.32509732e-01],
[-2.94841818e-01, -1.31979479e-01, 1.94384000e-01,
1.32509732e-01],
[-4.16009689e-01, -1.28296331e+00, 1.37546573e-01,
1.32509732e-01],
[-4.16009689e-01, -1.05276654e+00, 3.64896281e-01,
8.77547895e-04],
[ 3.10997534e-01, -1.31979479e-01, 4.78571135e-01,
2.64141916e-01],
[-5.25060772e-02, -1.05276654e+00, 1.37546573e-01,
8.77547895e-04],
[-1.02184904e+00, -1.74335684e+00, -2.60315415e-01,
-2.62386821e-01],
[-2.94841818e-01, -8.22569778e-01, 2.51221427e-01,
1.32509732e-01],
[-1.73673948e-01, -1.31979479e-01, 2.51221427e-01,
8.77547895e-04],
[-1.73673948e-01, -3.62176246e-01, 2.51221427e-01,
1.32509732e-01],
[ 4.32165405e-01, -3.62176246e-01, 3.08058854e-01,
1.32509732e-01],
[-9.00681170e-01, -1.28296331e+00, -4.30827696e-01,
-1.30754636e-01],
[-1.73673948e-01, -5.92373012e-01, 1.94384000e-01,
1.32509732e-01],
[ 5.53333275e-01, 5.58610819e-01, 1.27429511e+00,
1.71209594e+00],
[-5.25060772e-02, -8.22569778e-01, 7.62758269e-01,
9.22302838e-01],
[ 1.52267624e+00, -1.31979479e-01, 1.21745768e+00,
1.18556721e+00],
[ 5.53333275e-01, -3.62176246e-01, 1.04694540e+00,
7.90670654e-01],
[ 7.95669016e-01, -1.31979479e-01, 1.16062026e+00,
1.31719939e+00],
[ 2.12851559e+00, -1.31979479e-01, 1.61531967e+00,
1.18556721e+00],
[-1.14301691e+00, -1.28296331e+00, 4.21733708e-01,
6.59038469e-01],
[ 1.76501198e+00, -3.62176246e-01, 1.44480739e+00,
7.90670654e-01],
[ 1.03800476e+00, -1.28296331e+00, 1.16062026e+00,
7.90670654e-01],
[ 1.64384411e+00, 1.24920112e+00, 1.33113254e+00,
1.71209594e+00],
[ 7.95669016e-01, 3.28414053e-01, 7.62758269e-01,
1.05393502e+00],
[ 6.74501145e-01, -8.22569778e-01, 8.76433123e-01,
9.22302838e-01],
[ 1.15917263e+00, -1.31979479e-01, 9.90107977e-01,
1.18556721e+00],
[-1.73673948e-01, -1.28296331e+00, 7.05920842e-01,
1.05393502e+00],
[-5.25060772e-02, -5.92373012e-01, 7.62758269e-01,
1.58046376e+00],
[ 6.74501145e-01, 3.28414053e-01, 8.76433123e-01,
1.44883158e+00],
[ 7.95669016e-01, -1.31979479e-01, 9.90107977e-01,
7.90670654e-01],
[ 2.24968346e+00, 1.70959465e+00, 1.67215710e+00,
1.31719939e+00],
[ 2.24968346e+00, -1.05276654e+00, 1.78583195e+00,
1.44883158e+00],
[ 1.89829664e-01, -1.97355361e+00, 7.05920842e-01,
3.95774101e-01],
[ 1.28034050e+00, 3.28414053e-01, 1.10378283e+00,
1.44883158e+00],
[-2.94841818e-01, -5.92373012e-01, 6.49083415e-01,
1.05393502e+00],
[ 2.24968346e+00, -5.92373012e-01, 1.67215710e+00,
1.05393502e+00],
[ 5.53333275e-01, -8.22569778e-01, 6.49083415e-01,
7.90670654e-01],
[ 1.03800476e+00, 5.58610819e-01, 1.10378283e+00,
1.18556721e+00],
[ 1.64384411e+00, 3.28414053e-01, 1.27429511e+00,
7.90670654e-01],
[ 4.32165405e-01, -5.92373012e-01, 5.92245988e-01,
7.90670654e-01],
[ 3.10997534e-01, -1.31979479e-01, 6.49083415e-01,
7.90670654e-01],
[ 6.74501145e-01, -5.92373012e-01, 1.04694540e+00,
1.18556721e+00],
[ 1.64384411e+00, -1.31979479e-01, 1.16062026e+00,
5.27406285e-01],
[ 1.88617985e+00, -5.92373012e-01, 1.33113254e+00,
9.22302838e-01],
[ 2.49201920e+00, 1.70959465e+00, 1.50164482e+00,
1.05393502e+00],
[ 6.74501145e-01, -5.92373012e-01, 1.04694540e+00,
1.31719939e+00],
[ 5.53333275e-01, -5.92373012e-01, 7.62758269e-01,
3.95774101e-01],
[ 3.10997534e-01, -1.05276654e+00, 1.04694540e+00,
2.64141916e-01],
[ 2.24968346e+00, -1.31979479e-01, 1.33113254e+00,
1.44883158e+00],
[ 5.53333275e-01, 7.88807586e-01, 1.04694540e+00,
1.58046376e+00],
[ 6.74501145e-01, 9.82172869e-02, 9.90107977e-01,
7.90670654e-01],
[ 1.89829664e-01, -1.31979479e-01, 5.92245988e-01,
7.90670654e-01],
[ 1.28034050e+00, 9.82172869e-02, 9.33270550e-01,
1.18556721e+00],
[ 1.03800476e+00, 9.82172869e-02, 1.04694540e+00,
1.58046376e+00],
[ 1.28034050e+00, 9.82172869e-02, 7.62758269e-01,
1.44883158e+00],
[-5.25060772e-02, -8.22569778e-01, 7.62758269e-01,
9.22302838e-01],
[ 1.15917263e+00, 3.28414053e-01, 1.21745768e+00,
1.44883158e+00],
[ 1.03800476e+00, 5.58610819e-01, 1.10378283e+00,
1.71209594e+00],
[ 1.03800476e+00, -1.31979479e-01, 8.19595696e-01,
1.44883158e+00],
[ 5.53333275e-01, -1.28296331e+00, 7.05920842e-01,
9.22302838e-01],
[ 7.95669016e-01, -1.31979479e-01, 8.19595696e-01,
1.05393502e+00],
[ 4.32165405e-01, 7.88807586e-01, 9.33270550e-01,
1.44883158e+00],
[ 6.86617933e-02, -1.31979479e-01, 7.62758269e-01,
7.90670654e-01]])# 표준점수로 합점수를 계산
score = z.sum(axis=1)
scorescore 결과

# 표준화 공식 참고해서 값구해서 변수에 넣어서 직접 계산.
score.mean() # -1.7053025658242404e-15
score.std() # 2.7351140789959656
m = score.mean()
s = score.std()
z_score = (score - m) / s
z_score
T점수
표준화된 점수는 평균 0, 표준편차 1이므로 소수, 음수 등 익숙치 않은 값이 나온다.
> T점수 : 평균 50, 표준편차 10으로 좀 더 익숙한 범위의 값으로 변환
t_score = z_score * 10 + 50
# z_score * 표준편차 + 평균
t_score
Python에서 시각화하기
> 품종별 점수 범위
(T점수 기준)
import seaborn as sns
sns.boxplot(x=t_score, y=iris.species)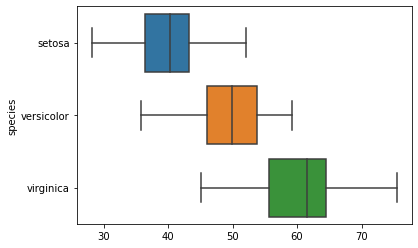
주성분 분석 Principal Component Analysis
선형 모형을 이용한 차원 축소
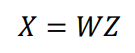
관찰된 데이터 X, 잠재 변수 Z, 계수 W
축을 회전시켜 새로운 축(성분)을 찾아내는 방법
• 분산이 큰 순서대로 성분을 정함
• 분산이 작은 성분들을 제거하여 차원을 축소
PCA는 가장 퍼져있는 방향으로 보여준다.
예) 화장품이 토너인지 패드인지 몰라도 PCA를 하면 구별이 돼서 보여줄 수 있다.
점수를 만들때 PCA를 하고서 만들면 좀 더 잘 구별되는 점수를 만들 수 있다.
Python에서 시각화하기
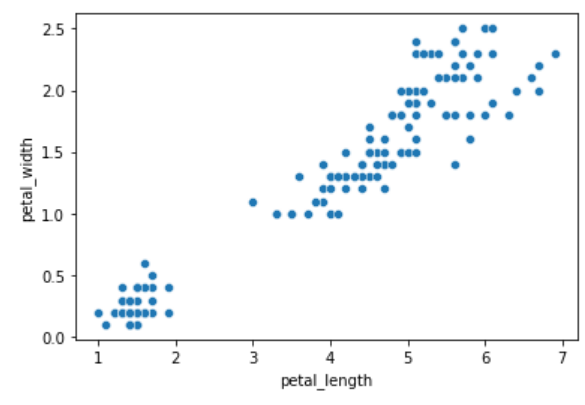
| import seaborn as sns sns.scatterplot(x='petal_length', y='petal_width', data= x) |
import seaborn as sns sns.scatterplot(x='sepal_length', y='sepal_width' , hue='species', data= iris) |
 |
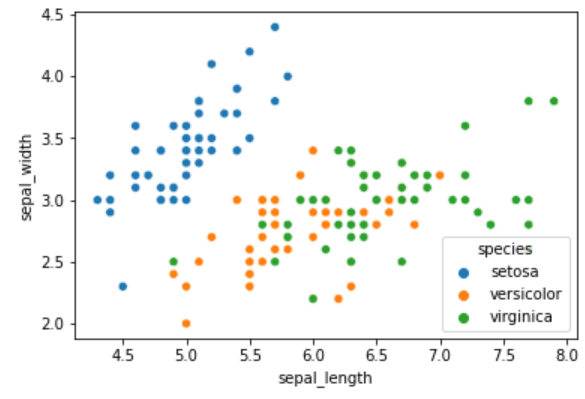 |
Python에서 PCA
from sklearn.decomposition import PCA
PCA(n_components = 개수)
> 품종별 점수 범위
from sklearn.decomposition import PCA
# 2차원 축소
pca = PCA(n_components =2)
pca.fit(x)
# 축소된 차원을 데이터로 변환
pc = pca.transform(x)
pc# pc
array([[-2.68412563, 0.31939725],
[-2.71414169, -0.17700123],
[-2.88899057, -0.14494943],
[-2.74534286, -0.31829898],
[-2.72871654, 0.32675451],
[-2.28085963, 0.74133045],
[-2.82053775, -0.08946138],
[-2.62614497, 0.16338496],
[-2.88638273, -0.57831175],
[-2.6727558 , -0.11377425],
[-2.50694709, 0.6450689 ],
[-2.61275523, 0.01472994],
[-2.78610927, -0.235112 ],
[-3.22380374, -0.51139459],
[-2.64475039, 1.17876464],
[-2.38603903, 1.33806233],
[-2.62352788, 0.81067951],
[-2.64829671, 0.31184914],
[-2.19982032, 0.87283904],
[-2.5879864 , 0.51356031],
[-2.31025622, 0.39134594],
[-2.54370523, 0.43299606],
[-3.21593942, 0.13346807],
[-2.30273318, 0.09870885],
[-2.35575405, -0.03728186],
[-2.50666891, -0.14601688],
[-2.46882007, 0.13095149],
[-2.56231991, 0.36771886],
[-2.63953472, 0.31203998],
[-2.63198939, -0.19696122],
[-2.58739848, -0.20431849],
[-2.4099325 , 0.41092426],
[-2.64886233, 0.81336382],
[-2.59873675, 1.09314576],
[-2.63692688, -0.12132235],
[-2.86624165, 0.06936447],
[-2.62523805, 0.59937002],
[-2.80068412, 0.26864374],
[-2.98050204, -0.48795834],
[-2.59000631, 0.22904384],
[-2.77010243, 0.26352753],
[-2.84936871, -0.94096057],
[-2.99740655, -0.34192606],
[-2.40561449, 0.18887143],
[-2.20948924, 0.43666314],
[-2.71445143, -0.2502082 ],
[-2.53814826, 0.50377114],
[-2.83946217, -0.22794557],
[-2.54308575, 0.57941002],
[-2.70335978, 0.10770608],
[ 1.28482569, 0.68516047],
[ 0.93248853, 0.31833364],
[ 1.46430232, 0.50426282],
[ 0.18331772, -0.82795901],
[ 1.08810326, 0.07459068],
[ 0.64166908, -0.41824687],
[ 1.09506066, 0.28346827],
[-0.74912267, -1.00489096],
[ 1.04413183, 0.2283619 ],
[-0.0087454 , -0.72308191],
[-0.50784088, -1.26597119],
[ 0.51169856, -0.10398124],
[ 0.26497651, -0.55003646],
[ 0.98493451, -0.12481785],
[-0.17392537, -0.25485421],
[ 0.92786078, 0.46717949],
[ 0.66028376, -0.35296967],
[ 0.23610499, -0.33361077],
[ 0.94473373, -0.54314555],
[ 0.04522698, -0.58383438],
[ 1.11628318, -0.08461685],
[ 0.35788842, -0.06892503],
[ 1.29818388, -0.32778731],
[ 0.92172892, -0.18273779],
[ 0.71485333, 0.14905594],
[ 0.90017437, 0.32850447],
[ 1.33202444, 0.24444088],
[ 1.55780216, 0.26749545],
[ 0.81329065, -0.1633503 ],
[-0.30558378, -0.36826219],
[-0.06812649, -0.70517213],
[-0.18962247, -0.68028676],
[ 0.13642871, -0.31403244],
[ 1.38002644, -0.42095429],
[ 0.58800644, -0.48428742],
[ 0.80685831, 0.19418231],
[ 1.22069088, 0.40761959],
[ 0.81509524, -0.37203706],
[ 0.24595768, -0.2685244 ],
[ 0.16641322, -0.68192672],
[ 0.46480029, -0.67071154],
[ 0.8908152 , -0.03446444],
[ 0.23054802, -0.40438585],
[-0.70453176, -1.01224823],
[ 0.35698149, -0.50491009],
[ 0.33193448, -0.21265468],
[ 0.37621565, -0.29321893],
[ 0.64257601, 0.01773819],
[-0.90646986, -0.75609337],
[ 0.29900084, -0.34889781],
[ 2.53119273, -0.00984911],
[ 1.41523588, -0.57491635],
[ 2.61667602, 0.34390315],
[ 1.97153105, -0.1797279 ],
[ 2.35000592, -0.04026095],
[ 3.39703874, 0.55083667],
[ 0.52123224, -1.19275873],
[ 2.93258707, 0.3555 ],
[ 2.32122882, -0.2438315 ],
[ 2.91675097, 0.78279195],
[ 1.66177415, 0.24222841],
[ 1.80340195, -0.21563762],
[ 2.1655918 , 0.21627559],
[ 1.34616358, -0.77681835],
[ 1.58592822, -0.53964071],
[ 1.90445637, 0.11925069],
[ 1.94968906, 0.04194326],
[ 3.48705536, 1.17573933],
[ 3.79564542, 0.25732297],
[ 1.30079171, -0.76114964],
[ 2.42781791, 0.37819601],
[ 1.19900111, -0.60609153],
[ 3.49992004, 0.4606741 ],
[ 1.38876613, -0.20439933],
[ 2.2754305 , 0.33499061],
[ 2.61409047, 0.56090136],
[ 1.25850816, -0.17970479],
[ 1.29113206, -0.11666865],
[ 2.12360872, -0.20972948],
[ 2.38800302, 0.4646398 ],
[ 2.84167278, 0.37526917],
[ 3.23067366, 1.37416509],
[ 2.15943764, -0.21727758],
[ 1.44416124, -0.14341341],
[ 1.78129481, -0.49990168],
[ 3.07649993, 0.68808568],
[ 2.14424331, 0.1400642 ],
[ 1.90509815, 0.04930053],
[ 1.16932634, -0.16499026],
[ 2.10761114, 0.37228787],
[ 2.31415471, 0.18365128],
[ 1.9222678 , 0.40920347],
[ 1.41523588, -0.57491635],
[ 2.56301338, 0.2778626 ],
[ 2.41874618, 0.3047982 ],
[ 1.94410979, 0.1875323 ],
[ 1.52716661, -0.37531698],
[ 1.76434572, 0.07885885],
[ 1.90094161, 0.11662796],
[ 1.39018886, -0.28266094]])# 시각화
import seaborn as sns
sns.scatterplot(x=pc[:, 0], y=pc[:,1], hue=iris.species)
# x=pc[:,0]만 사용하고 품종 정보를 쓰지 않았음에도 품종까지 구분이 가능해짐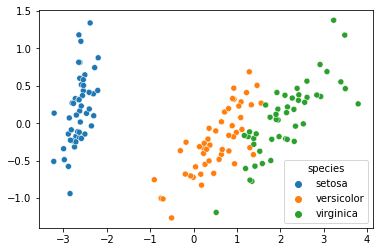
# 시각화
# 주성분 분석으로 해서 만든 새로운 점수로 시각화하면,
import seaborn as sns
sns.boxplot(x=pc[:,0], y=iris.species)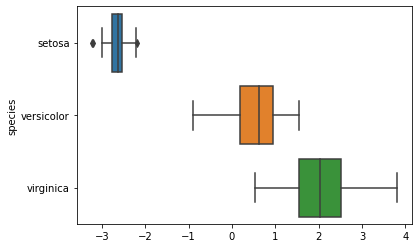
PCA 해석
• 가중치
: 원래 변수에 각각의 가중치를 곱하여 모두 더하면 새로운 차원의 값이 됨
pca.components_
• 설명된 분산의 비율
: 새로운 차원이 원래의 분산을 설명하는 비율
pca.explained_variance_ratio_
# 원래 변수에 가중치 곱해서 모두 더하면 새로운 차원의 값이 된다.
pca.components_
# array([[ 0.36138659, -0.08452251, 0.85667061, 0.3582892 ],
[ 0.65658877, 0.73016143, -0.17337266, -0.07548102]])# 설명된 분산의 비율
pca.explained_variance_ratio_
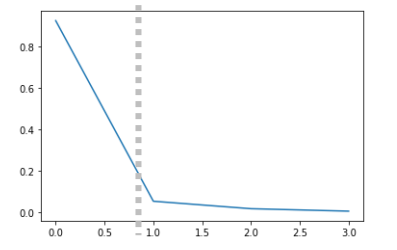
# array([0.92461872, 0.05306648])Scree plot
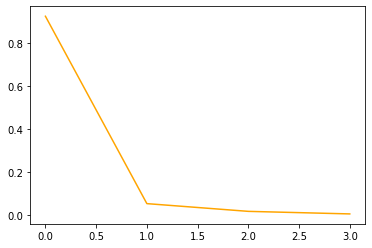
시각화의 경우, 2차원으로 축소
시각화 이외의 경우 적절한 차원을 결정할 때 scree plot 을 사용
• 설명된 분산의 비율이 완만하게 감소되는 차원들은 버림
예: 아래 그림의 경우 1차원으로 축소
import matplotlib.pyplot as plt
p = PCA(n_components=4)
p.fit(x)
plt.plot(p.explained_variance_ratio_, color='orange')| ▶ 오른쪽 구분선(점선) 이후로 분산의 비율이 완만하게 감소되는 차원은 버린다. | |
 |
 |
'기초통계' 카테고리의 다른 글
| [텍스트 분석] 자연어 : 문서 단어 행렬 (0) | 2022.10.04 |
|---|---|
| [차원축소와 군집분석] 군집분석 : Clustering (0) | 2022.10.04 |
| 상호작용과 인과 : 횡단 비교와 종단 비교 (0) | 2022.09.13 |
| 상호작용과 인과 : 인과효과 (0) | 2022.09.13 |
| 상호작용과 인과 : 상호작용 (0) | 2022.09.13 |