통계적 가설 검정
Karl Pearson, Ronald Fisher 등 통계학의 초기 인물들이 개발한 절차
< 실증주의>
• 반증주의 철학에 기반하고 있어 일반적인 과학적 가설 검정과 다르며,
많은 비판이 있었으나, 오랫동안 쓰여왔기 때문에 여전히 널리 쓰임.
통계적 가설 검정의 절차
귀무가설 수립 → 유의수준(α) 결정 → p-값 계산 → p값과 유의수준 비교
(1) 귀무가설 수립
• 귀무가설 null hypothesis
: 기각하고자 하는 가설
• 대립가설 alternative hypothesis
: 주장하고자 하는 가설
(2) 유의수준 결정
• 유의 수준 (α) significance level
: (100% - 신뢰수준)
(3) p-값 계산
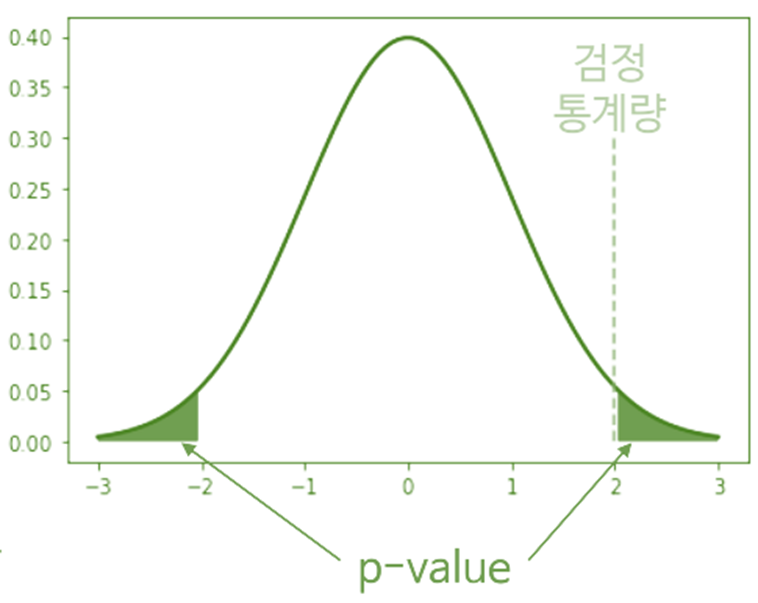
• p-값 : 귀무가설이 참일 때 검정통계량 이상이 나올 확률
실험이나 관찰에서 나온 값이 얼마나 유의한지 평가한 값
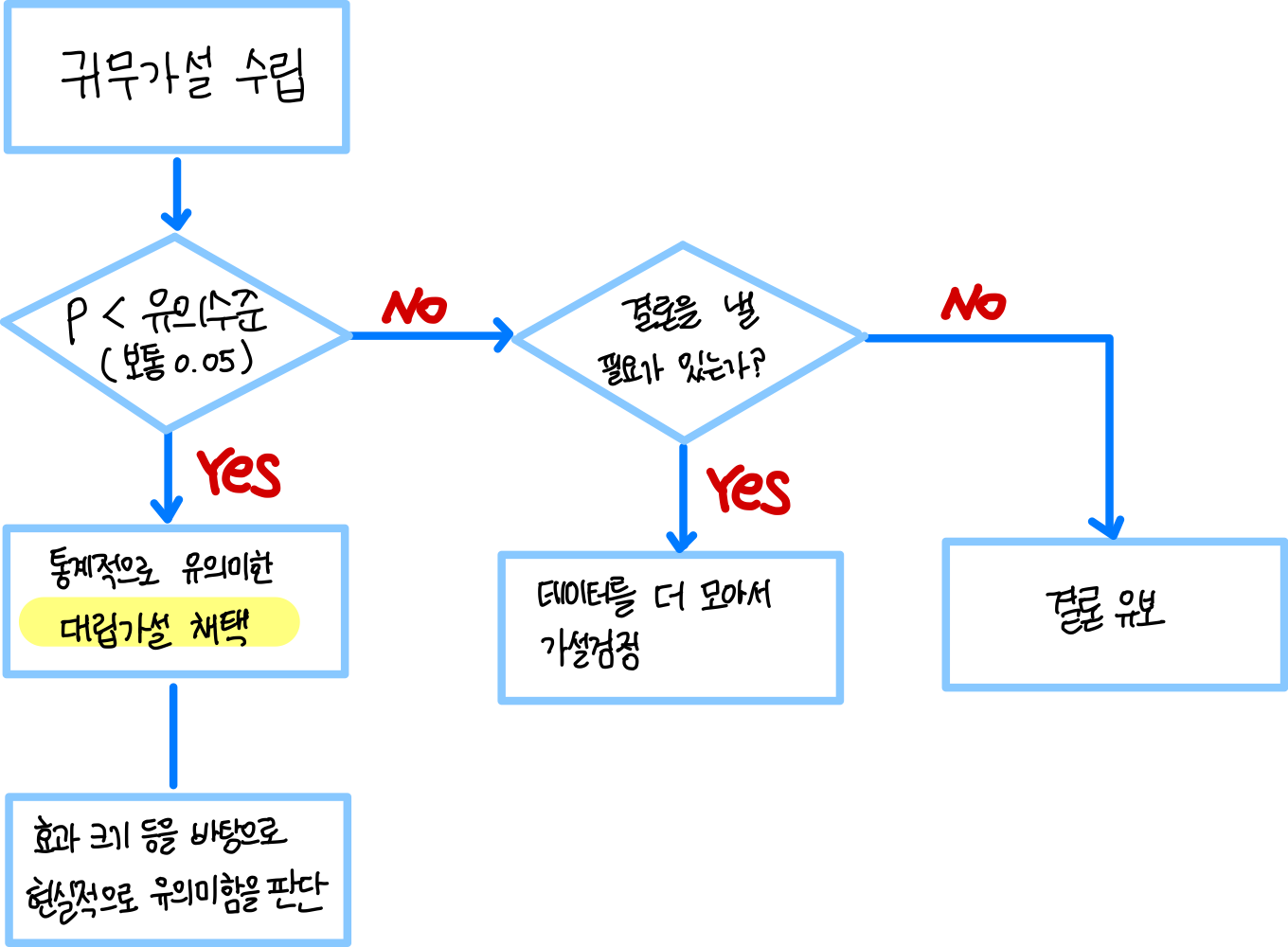
(4) p값과 유의수준 비교
| p -val > 유의수준 | p -val < 유의수준 |
| • 결론을 유보한다. • 결론을 내릴 필요가 있을 경우, 데이터를 더 모은다 • 단, 반복해서 가설검정을 할 경우 유의수준을 조정한다. |
• 귀무가설을 기각한다 • 흔히 "통계적으로 유의하다"라고 표현 (현실적으로 유의미한 것은 아님) |
import pingouin as pg
pg.ttest(hr.rating, 3.0)ttest에서 컬럼 다음 0 이 뜻하는 것(=hr.rating의 평균이 0이다.) 이 바로 귀무가설이다.
'rating 평균이 3.0일 것이다 ' 라고 가정했는데, p-val < 0.05이므로 귀무가설 기각

통계적 가설검정에서 귀무가설은 채택하지 않는다
즉, 까고 싶은 걸 절대 인정하지 않는 것.
import pingouin as pg
pg.ttest(hr.rating, 2.8)
유의수준은 내 마음속 기준
· 구간추정 : 표본통계량 -> 모수 추정
· 가설검정 : 모수에 대한 귀무가설 -> 표본 통계량에 비추어서 귀무가설을 기각한다.
<참고 사이트>
https://www.tandfonline.com/doi/full/10.1080/00031305.2016.1154108
The ASA Statement on p-Values: Context, Process, and Purpose
Published in The American Statistician (Vol. 70, No. 2, 2016)
www.tandfonline.com
| 실제 가설검정 | 귀무가설 기각 | 귀무가설 채택 |
| 귀무가설이 참 | 1종 오류 False Alarm |
|
| 귀무가설이 거짓 | 2종 오류 Miss |
1종오류와 2종오류
예시
- 1종 오류 : 유의수준이 빡빡하면 착한 사람들이 잡혀들어간다.
- 2종 오류 : 유의수준을 낮추면 나쁜사람들이 풀려나게 된다.
유의수준이 0% 면 2종 오류가 미친듯이 증가하게 된다.
Python에서 평균의 가설검정
> '귀무가설'이 모평균 900 일 때,
import pandas as pd
df = pd.read_excel('car.xlsx')
import pingouin as pg
pg.ttest(df.price, 900, confidence=0.95)
p-val < 0.05 이므로 귀무가설이 기각되고 통계적으로 유의미하다 할 수 있다.
가설검정과 신뢰구간의 관계
• 통계적 가설검정과 신뢰구간은 동일한 이론의 양면
> 95% 신뢰구간이 귀무가설의 모수를 포함하지 않으면, 5% 유의수준에서 가설검정은 귀무가설을 기각한다.
p-value 에 영향을 주는 요소들
• 관찰된 통계량이 귀무가설에서 멀리 떨어져 있으면 p-value가 작아짐
• 표본의 크기가 크면 p-value가 작아짐
통계적 유의함 statistical significance
• 통계적 가설검정에서 귀무가설을 기각하는 경우 " 통계적으로 유의하다 "라고 함
• 동일한 관계의 변수라도 표본이 크면 p-value가 작아지고, 통계적으로 유의하게 됨
• 어떠한 관계가 있다고 주장하기에 표본의 크기가 충분하다는 것으로 이해할 수 있음
• 현실적으로 유의미함을 의미하는 것으로 오해하지 말 것
• 현실적 유의미함은 가치 판단의 대상
'기초통계' 카테고리의 다른 글
| [기초통계] 집단 비교 : 독립표본 t검정, 검정력, 효과크기, 분산분석, 분할표 (0) | 2022.08.18 |
|---|---|
| [기초통계] A/B 테스트 (0) | 2022.08.18 |
| 확률과 통계 II : 모집단, 표본 그리고 표집 (0) | 2022.08.16 |
| 확률과 통계 I (0) | 2022.08.16 |
| 실험설계 (0) | 2022.07.26 |