확률과 통계 I
사례와 변수
• 사례 case
데이터 수집의 단위 (예: 고객, 제품, …)
• 변수 variable
사례에 따라 달라지는 값 (예: 나이, 가격, …)
데이터를 표로 정리해보면,
• 행(row) : 표에서 가로 방향 한 줄/ 하나의 사례
• 열(column) :표에서 세로 방향 한 줄 / 하나의 변수
변수
변수 ?
범주형 변수
종류, 이름 등에 해당한다.
• 숫자로 표시하더라도 양적인 개념이 아니며, 덧셈 등 대부분의 연산이 의미가 없음
즉, 범주형 변수는 평균을 내면 안된다.
• 순서가 있을 수도 있으나, 간격이 일정하지 않음
예: 주거 형태, 고향, 학력, 출석
연속형 변수
연속적인 형태
정수나 실수로 표현할 수 있는 것
• 간격이 일정하고 덧셈, 뺄셈 등의 계산이 의미가 있음
예: 무게, 나이, 시간, 거리, 자녀의 수, 시험 점수
통계의 종류
기술 통계
descriptive statistics
: 데이터를 묘사, 설명
• 데이터를 묘사, 요약, 설명하는 통계적 방법과 절차
• 기술 통계치 :
- 중심 경향치
- 분위수
- 변산성 측정치
추론 통계
inferential statistics
: 데이터를 바탕으로 추론, 예측
통계학의 대부분은 추론 통계이다.
기술 통계치
중심 경향치 (Central tendency)
데이터가 어디에 몰려있는가?
• 종류 : 평균, 중간값, 최빈값
평균 (mean)
N개의 값이 있을 때, 그 합계를 N으로 나눈 것
• 평균은 극단값에 따라 영향을 크게 받는다.
10, 20, 30, 40, 50이 있을 경우 → 30
10, 20, 30, 40, 500이 있을 경우 → 120
중간값 (median)
값들을 크기 순으로 정렬했을 때 중간에 위치한 값
10, 20, 30, 40, 50의 중간값 → 30
10, 20, 30, 40, 500의 중간값 → 30
"중위수"라는 표현도 많이 사용 (중위소득, 중위가격 등)
• 값이 짝수개 있을 경우는 가운데 두 값의 평균
10, 20, 30, 40의 중간값 → 20과 30의 평균 → 25
보완하는 지표로 많이 쓰인다.
최빈값 (mode)
가장 많은 사례에서 관찰된 값
mode ; 상태, 유행, 가장 많은 것
• 연속 변수보다는 범주형 변수에서 유용
예: 직원 중에 김씨가 30%가 가장 많음
• 연속 변수의 경우 구간을 나누어 최빈값을 구하는 경우가 많음
예: 고객 중에 30대가 25%로 가장 많음
• 구간을 나누는 방법에 따라 최빈값이 달라질 수 있음
연습
연습파일 car.xlsx

import pandas as pd
df = pd.read_excel('car.xlsx')
print(df.mileage.mean()) # 평균
print(df.mileage.median()) # 중앙값
print(df.mileage.mode()) # 최빈값df.model.value_counts() # model의 범주별 빈도분위수 (Quantile)
크기순으로 정렬된 데이터를 q개로 나누는(분) 위치의 값
• 종류 : 사분위수, 백분위수 등
사분위수 (Quartile)
데이터를 4등분하는 위치
제1사분위수 → 1/4 지점
제2사분위수 → 2/4 지점
제3사분위수 → 3/4 지점
* 영어 철자에 주의. 분위수(quantile), 사분위수(quartile)
백분위수 (percentile)
데이터에서 순위를 퍼센트로 표현
최소값 = 0퍼센타일
제1사분위수 = 25퍼센타일
제2사분위수 = 중간값 = 50퍼센타일
제3사분위수 = 75퍼센타일
최대값 = 100퍼센타일
연습
분위수 .quantile(분위)
df.price.quantile(0) # 가격순 1등(가장 저렴한 차)
df.price.quantile(0.5) # 가격순 중간
df.price.quantile(1) # 가격순 꼴찌
df.price.quantile(0.1) # 가격순 상위 10% 저렴한 차데이터 값에 대한 분위수를 찾고 싶다면,
import scipy.stats
scipy.stats.percentileofscore(df.price, 1320) # 89.96350364963503변산성 측정치
데이터가 퍼져 있는 정도를 나타내는 수치
• 종류 : 범위, 사분위수범위, 분산, 표준편차
범위 (range)
최대값 – 최소값
예: 10, 20, 30, 40, 50의 경우 최대값(50) – 최소값(10) = 40
극단값이 있으면 커짐
예: 10, 20, 30, 40, 500의 경우 490
사분위간 범위 (InterQuartile Range)
(제3사분위수 - 제1사분위수)
IQR이라고 불림.
극단값은 최소값 또는 최대값 근처에 있으므로 극단값의 영향이 적음
상자수염그림 (box-whisker plot)
제1사분위수 ~ 제3사분위수를 상자로 표현
• 중간값은 상자의 가운데 굵은 선으로 표시
• 최소값과 최대값은 수염(whisker)으로 표시
• 수염의 최대 길이는 IQR의 1.5배까지, 넘어가는 경우는 점으로 표시

연습
시각화패키지 seaborn 패키지 .boxplot
import seaborn as sns
sns.boxplot(x='price', data=df)
sns.boxplot(x='price', y='model', data=df)
편차 (deviation)
( 값 – 평균 )
예: 원 데이터가 30, 40, 50인 경우, 평균은 40, 편차는 -10, 0, +10
분산 (deviation)
편차 제곱의 평균
직관적으로 이해하기는 어려우나 수학적으로 중요한 여러 성질이 있음
편차를 제곱하여 크기가 커지므로 표준편차(√분산)를 많이 사용
연습
분산 .var() 표준편차 .std()
df.price.var() # 분산 110631.49243335734
df.price.std() # 표준편차 332.6131272715455
히스토그램
(histogram)
데이터를 구간별로 나눠, 각 구간의 사례 수를 막대그래프로 그린 것.
연습
시각화패키지 seaborn 패키지 .histplot()
sns.histplot(x='price', data=df, color='yellow')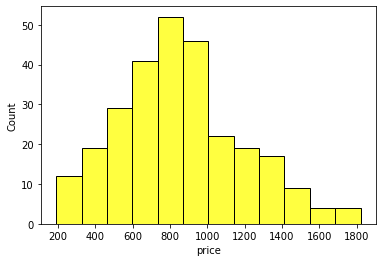
히스토그램 막대 개수 조정 bins
sns.histplot(x='price', data=df, bins = 20, color='yellow')
import matplotlib.pyplot as plt
xs = list(range(100, 2100, 200))
sns.histplot(x='price', data=df, bins=xs, color='yellow')
커널 밀도 추정
(kernel density estimation)
데이터의 밀도를 추정하여 그린 곡선
kde = True 로 설정할 수 있다.
import matplotlib.pyplot as plt
xs = list(range(100, 2100, 200))
sns.histplot(x='price', data=df, bins=xs, color='orange', kde=True)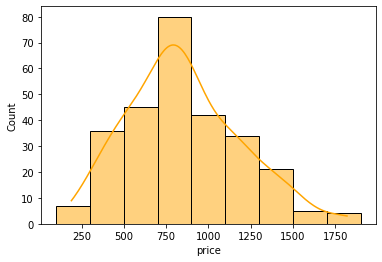
'기초통계' 카테고리의 다른 글
| [기초통계] 집단 비교 : 독립표본 t검정, 검정력, 효과크기, 분산분석, 분할표 (0) | 2022.08.18 |
|---|---|
| [기초통계] A/B 테스트 (0) | 2022.08.18 |
| [기초통계] 통계적 가설 검정 (0) | 2022.08.18 |
| 확률과 통계 II : 모집단, 표본 그리고 표집 (0) | 2022.08.16 |
| 실험설계 (0) | 2022.07.26 |