집단비교
A/B 테스트와 MVP를 만들어 실험을 했다.
그럼 통계적으로는 어떻게 분석해야 할까?
Multi - Armed Bandit 솔루션
딜레마를 해결하기 위해
대규모 서비스 같은 경우에는 이 솔루션을 사와서 실험 추이를 보며 리소스 통제 계획을 정한다.
예) optimizely
집단 비교 통계 처리 순서도
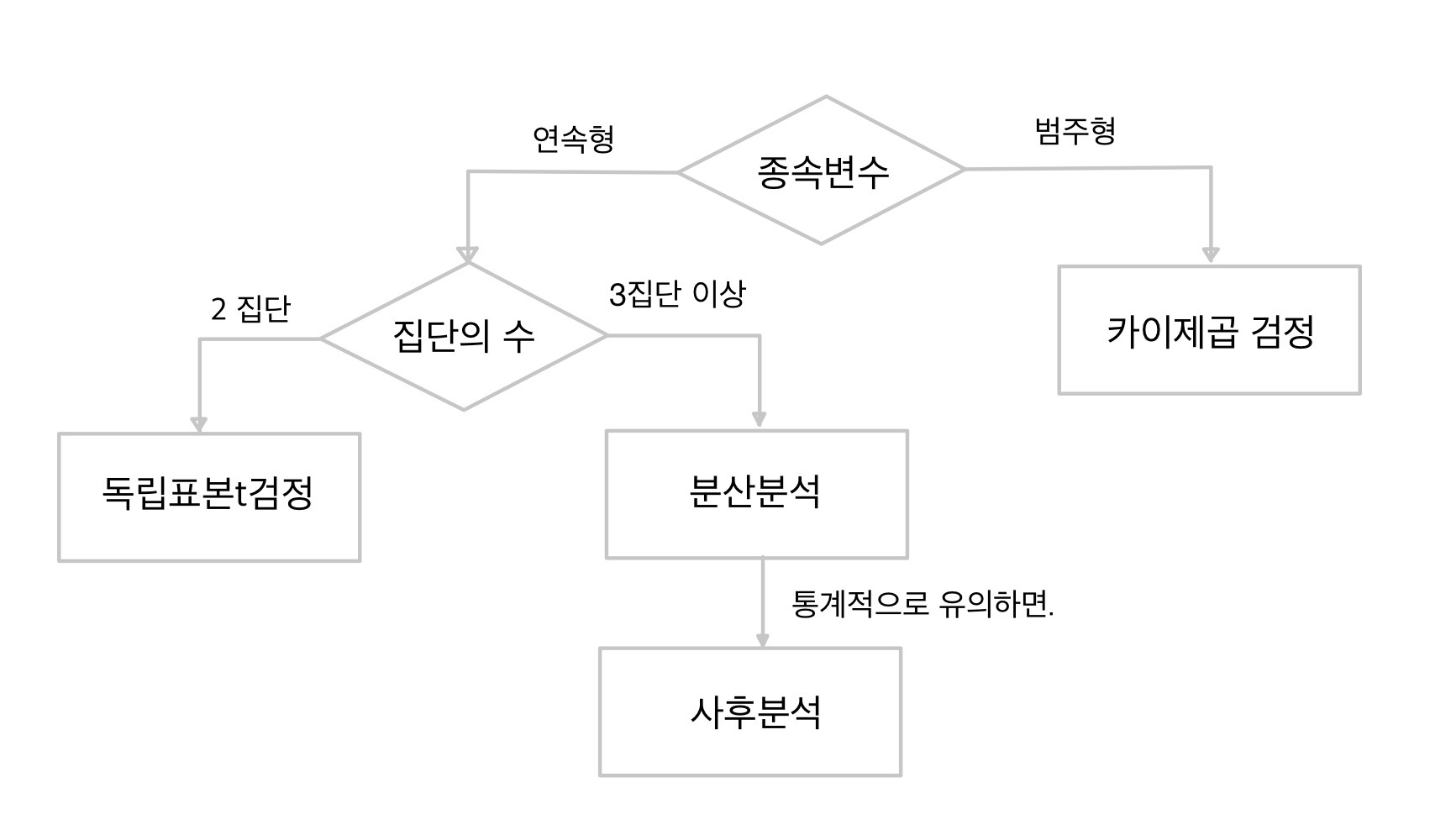
'종속변수'의 예
- A와 B군중 어디가 매출이 더 잘 나오는가? > 매출은 연속된 값 > 연속형
- 가입을 하느냐, 탈퇴를 하느냐? > 가입 아니면 탈퇴 > 범주형
독립표본 t-검정
두 집단의 평균 차이
𝑋1: 대조군 평균
𝑋2: 실험군 평균
• 두 집단의 모집단이 모두 정규분포를 따르거나, 또는 각 집단의 크기가 충분히 큰 경우 (𝑛 > 30)
t-분포를 이용해서(𝑋1 − 𝑋2)의 신뢰구간을 계산
• 가설검정의 경우 독립표본 t-검정을 수행
Python에서 독립표본 t-검정
car.xlsx 데이터 활용
car = pd.read_excel("car.xlsx") # xlsx 파일 읽어오기 : pd.read_excel()
k3 = car.price[car.model == 'K3'] # k3 가격
avante = car.price[car.model == 'Avante'] # Avante 가격
k3.mean() # k3 가격 평균 913.8115942028985 원
avante.mean() # Avante 가격 평균 833.4146341463414 원 표본에서는 K3가 Avante보다 평균 80만원 더 비쌋다.
그러면모집단에서도 그럴까?
·귀무가설 : k3와 avante, 두 집단의 평균이 같다.
· 신뢰구간 : k3와 avante의 '평균 차이'의 신뢰구간
혹은 두 평균의 차이의 가설검정을 구하면 된다.
import pingouin as pg
pg.ttest(k3, avante) # k3, avante 두 집단의 평균에 대한 차이를 구하는 독립표본 t검정 실시
| 구분 | 설 명 |
| T | 검정통계량 |
| dof | 자유도 |
| tail | |
| p-val | p-value |
| CI95% | 신뢰구간 |
| cohen-d | 코헨의 d |
| BF10 | |
| power | 검정력 |
( k3 평균 - Avante 평균 ) 이 적게는 8만원부터 최대 152만원까지 차이가 날 수 있다.
귀무가설은 모집단에서 평균의 차이가 0. (즉 k3평균 = Avante 평균)
귀무가설은 기각되고 'k3는 Avante보다 비싸다' 라고 결론지을 수 있다.
연습
single과 married의 rating 평균은 차이가 있을까?
# 데이터 불러오기
import pandas as pd
import numpy as np
hr = pd.read_excel('c:\\data\\hr.xlsx')
# 결혼 여부 컬럼값 확인하기
hr.marriage.value_counts()
"""
single 763
married 707
Name: marriage, dtype: int64
"""
# marriage 컬럼에 'single'과 'marriage'의 만족도를 두 집단으로 분류한다.
single_r = hr.rating[hr.marriage == 'single']
married_r = hr.rating[hr.marriage == 'married']
# 두 집단의 평균 차이에 대한 가설검정
import pingouin as pg
pg.ttest(single_r, married_r)
# pg.ttest(k3, 800) : k3의 평균이 800인가? 를 검정
# pg.ttest(k3, avante) : k3 평균과 avante의 평균이 같은가? 를 검정
p-val가 아주 작다 → 귀무가설을 기각한다.
귀무가설 > single과 married와 평균이 같다.
import seaborn as sns
sns.kdeplot(x='rating', hue='marriage', data=hr, bw_adjust=2.0)
# hue 카테고리 변수이름
# bw_adjust < 그래프 매끄럽게 보는 코드

평균이 아닌 다른 것을 비교할 수도 있다.
맨 휘트니 U검정
pg.mwu(married_r, single_r) # 무작위로 기혼자와 미혼자 중에 한명씩 뽑았을 때
# 귀무가설 : P(기혼자 > 미혼자) = P(기혼자 < 미혼자)
> p-val 가 작으므로 귀무가설은 기각한다.
어디에 쓰일 수 있나?
> 두 집단 비교할 때
· 신약 개발
신약 vs 플라시보(가짜약) 의 회복 기간을 비교한다
평균5일 평균7일
· 제품
신제품 vs 경쟁제품
만족도3.8 2.9
독립표본 t 검정 순서도

검정력 power
• 유의수준(𝛼) :귀무가설이 참일 때, 기각하는 1종 오류의 확률
• 𝛽 : 귀무가설이 거짓일 때, 기각하지 못하는 2종 오류의 확률
• 검정력(1 − 𝛽) : 귀무가설이 거짓일 때, 이를 올바르게 기각할 확률
- 보통 검정력은 0.8 이상을 요구
검정력이 낮은 예)

표본의 크기가 크면 증가
분석 결과에 나오는 검정력은 모수가 통계량과 같다는 가정 아래 계산됨.
효과 크기 effect size
관찰된 현상의 크기를 나타내는 방법
• 방법:
분산을 이용하는 방법 > 에타제곱
평균 차이를 이용하는 방법 > 코헨의 d
에타 제곱 𝜂² eta squared 코헨의 d Cohen's d
• 분산을 이용한 효과 크기 표현 방법 • 전체 SS = (X – 전체평균)²의 합계 • 처치 SS = (집단평균 - 전체평균)²의 합계 • SS : 편차제곱합(Sum of Squares) |
• 두 집단의 평균 차이를 데이터의 표준편차로 나눈 것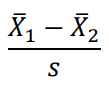 • 평균 차이의 크기를 알기 쉽게 나타낸 것 •t-test 하면 쉽게 확인할 수 있다. |
| • 에타 제곱 = 1 • 집단 간 차이만 있고 집단 내 차이는 없음 • 실험 조건에 따라 모든 것이 달라짐 • 실험 조건이 같으면 결과도 같음 • 에타 제곱 = 0 • 집단 간 차이는 없고 집단 내 차이만 있음 • 실험 조건에 따라 아무 것도 달라지지 않음 • 같은 실험 조건에도 서로 다름 |
|
| 예)대조군 데이터는 1, 1, 1이고, 실험군 데이터는 3, 3, 3인 경우 • 집단 내 차이는 없고, 집단 간 차이만 존재 • 에타 제곱 = 1 예) 대조군 데이터는 1, 2, 3이고, 실험군 데이터도 1, 2, 3인 경우 • 집단 내 차이만 있고, 집단 간 차이는 없음 • 에타 제곱 = 0 |
예) 친구와 나의 IQ 검사 1표준편차 = 15점 나 100 친구 115 → Cohen's d 1 나 120 친구 123 → Cohen's d 0.24 |
*에타제곱< R² 와 같은 개념.
▶ 효과크기 계산
import pingouin as pg
pg.compute_effsize( 집단1, 집단2, eftype='방법')
• 에타 제곱 eta-square
pg.compute_effsize(avante, k3, eftype='eta-square')• 코헨의 d cohen
pg.compute_effsize(avante, k3, eftype='cohen')분산분석
• 집단 간 차이가 크다면 집단 내 분산에 비해 집단 간 분산이 커질 것
• 모집단이 정규분포를 따르거나,
각 집단의 표본 크기가 충분히 크면 집단 간분산/집단 내분산의 비율은 F 분포를 따름
이를 통해"모든 집단들의 평균이 같다"는 귀무가설을 검정할 수 있음.
• 귀무가설을 기각할 경우, "적어도 한 집단의 평균은 다르다"라는 대립가설을 채택
분산분석 순서도

Python 분산 분석
pg.anova(dv=' ', between=' ', data= , detailed=True/False)
car = pd.read_excel("car.xlsx")
import pingouin as pg
pg.anova(dv='price', between='model', data=car, detailed=True)- 집단간 분산분석 p-val = 0.082432
집단 간 집단 내 |
검정통계량 p-value 에타제곱 |
ttest는 원래 두 집단의 분산이 같아야 한다. (분산을 보정하는 과정이 들어간다.)
서로 분산이 다르면 분산을 보정해주는데 (correction=True)
이 보정 옵션을 제거하면 분산분석과 동일한 p-val이 나오게 된다.
# 보정 옵션을 끄면 ttest의 p-val와 분산분석의 p-val는 같다.
pg.ttest(k3, avante, correction=False)
ttest에서 보정 옵션을 주지 않으면, 두 집단의 분산이 같은지 먼저 가설검정을 한다.
이 가설검정이 기각되면, 자동 보정이 된다. 기각이 안되면 보정 별도로 하지 않음.
pg.ttest(k3, avante)
anova는 수동 보정이 필요하다.
pg.welch_anova()
pg.welch_anova(dv='price', between='model', data=car)다중비교 multiple comparison
• 분산 분석은 한 번에 여러 집단을 비교할 수 있음.
• 독립표본 t-검정은 한 번에 두 집단만 비교 가능.
• 집단이 여러 개 있을 경우 독립표본 t-검정은 집단 간의 모든 짝을 비교해야 함.
- 집단이 k개일 경우 필요한 비교 횟수 = k(k-1) / 2
연습
Python 집단별 평균 확인
import pandas as pd
st = pd.read_csv('student-mat.csv')
st.groupby('Mjob').agg({'G3':'mean'})
CASE1 )집단 간 분산이 같은 데이터
① 데이터 import 하기
import pandas as pd
st = pd.read_csv("student-mat.csv")
st.head()
② 집단 간 분산이 같은지 확인하기 :Levene 검정
pg.homoscedasticity(dv=' ', group=' ', data= )
import pingouin as pg
pg.homoscedasticity(dv='G3', group='Mjob', data=st)
# G3 = 학점, Mjob = 어머니 직업
# 귀무가설 : Mjob(어머니 직업)별 학생 집단의 G3(학점) 분산이 같다.
③ 집단 간 분산이 같다면 Tukey HSD검정, 같지 않다면 Pairwise_gameshowell 검정
# 분산분석
pd.anova(dv='G3', between='Mjob', data=st)
> p-value가 0.05 보다 작으므로 귀무가설은 기각된다.
즉, Mjob에 따라 나누어진 학생 집단중 G3의 평균이 같지 않은 집단이 있을 수 있다.
④집단 간 분산이 같으므로 Tukey HSD 검정선택
import pingouin as pg
pg.pairwise_tukey(dv='G3', between='Mjob', data=st)
# hedges : cohen-d와 비슷한 개념
# p-tukey : p-value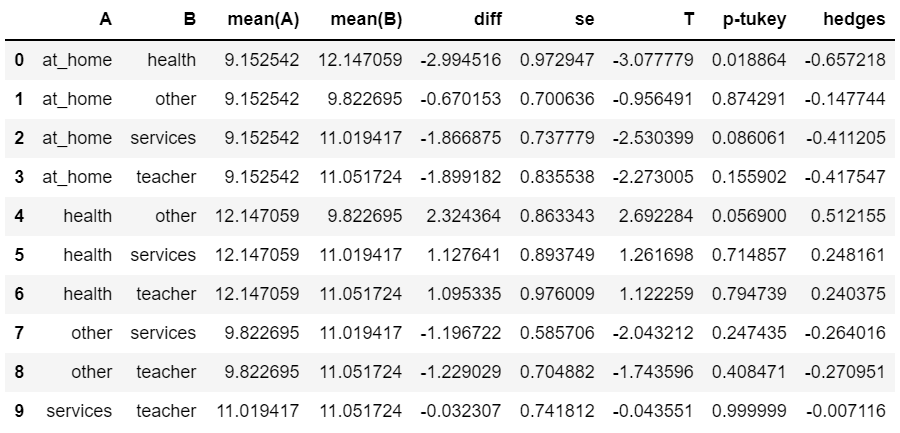
CASE2 )집단간 분산이다른데이터
① 데이터 import 하기
import pandas as pd
hr = pd.read_csv("c:\\data\\hr.xlsx")
hr.head()

② 집단 간 분산이 같은지 확인하기
: agg()메소드 사용
hr.groupby('job_level').agg({'rating':'var'})
: pg.homoscedasticity(dv=' ', group=' ', data= )
pg.homoscedasticity(dv='rating', group='job_level', data=hr)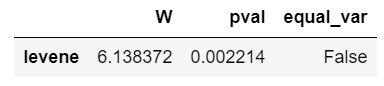
>집단 간 분산이 다른 집단이 존재한다.
③ 분산분석 : 분산이 같지 않을 때
import pingouin as pg
pg.welch_anova(dv='rating', between='job_level', data=hr)
np2< 에타 제곱
0-1 사이
0 : 전혀 영향력이 없음 ~
1 : 영향력이 매우큼
④ 집단 간 분산이 다르므로 gameshowell 검정 선택
pg.pairwise_gameshowell(dv='raing', between='job_level', data=hr)
FWER Familywise Error Rate
다중 비교를 할 경우,적어도 한 번1종 오류가 발생할 확률
예) 세 집단이 모집단에서 평균이 모두 같은 경우
유의수준(𝛼)5%인 비교를 3번해서,3번 모두 1종 오류를 피할 확률(독립적이라고 가정할 경우):
95% × 95% × 95 % ≈ 86%
바꿔 말하면적어도 한 번 1종 오류가 발생할 확률(FWER)은 14%
비교를 많이 할수록 FWER은 증가
사후 검정 post hoc test
FWER을 통제하기 위해분산 분석을 먼저 실시한다.
분산 분석 결과가 통계적으로 유의하면( 𝑝 < 𝛼 ) 사후 검정을 실시
• 여러 집단 중 통계적으로 유의한 차이가 나는 집단을 식별
• 사후 검정에서도 𝛼를 조절하여 FWER이 커지지 않도록 제어
- 각 집단의 분산이같은경우:Tukey HSD
- 각 집단의 분산이다른경우:Games-Howell검정
등분산성 homoscedasticity
집단간 분산이 같은지는Levene 검정으로 확인 가능
🤷🏻♀️ 등분산성을 확인하고 바로 tukey 나 Gameshowell 검정을 하지 않는 이유?
Gameshowell이나 Tukey는 유의수준이 5% 가 된다는 보장이 없다.
최대한 유의수준이 5% 가 되도록 보정이 들어가 있긴 하지만 보장은 되지 않는다.
하지만 anova는 이게 가능하다.
anova에서 귀무가설 기각
→ 제대로 기각
→ 잘못 기각 (1종 오류) 5%
anova에서 잘 판단하면,다음 단계에서 tukey나 gameshowell을 해서 틀려도 이미 anova에서 잘못 기각됐기 때문에(1종 오류) 의미가 없다.즉 엄격하게 먼저 판단을 한다.
분할표 contingency table
행과 열이 서로 다른 범주형 변수의 값을 나타내는 표.
.pivot_table( index = ' ', columns = ' ' , aggfunc = 'size' )
• 범주형 변수의 값에 대한 사례 수 (size)를 표기해준다.
: 결혼 여부와 부서에 대한 사례수를 표기함.
import pandas as pd
hr = pd.read_excel("c:\\data\\hr.xlsx")
hr.pivot_table(index='marriage', columns='department', aggfunc='size')
위에는 표본집단.
모집단에서도 재무부서가 결혼 비율이 높다고 할 수 있나?
부서별로 결혼한 사람의 비율의 차이가 있을까?
= 결혼한 사람들 중에 부서별 비율이 차이가 있을까?
>가설 검정이 필요하다.
이 때 필요한 검정이'카이제곱 검정'
카이제곱 검정
두 범주형 변수가 독립적이라는 귀무가설을 검정
예) 부서와 결혼
H0: 부서별 결혼 비율이같다
H1: 부서별 결혼 비율이 다르다
• 데이터가 적으면 p-value가 부정확할 수 있음.
• 기대 빈도(expected)가 5 이하인 경우가 20% 이하를 권장
• Cramér's V: 두 변수의 관계를 0~1로 표시
- 0 : 전혀 관련이 없음
- 1 : 완전히 일치
카이제곱 검정 순서도

Python에서 카이제곱검정
pg.chi2_independence( x=' ', y=' ', data= )
import pingouin as pg
# 카이제곱 검정
expected, observed, stats = pg.chi2_independence( x='marriage', y='department', data=hr)| 귀무가설이 참이라면 예상되는expected 값 = 기대빈도 | observed 관측값 |
 |
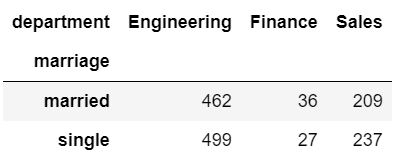 |
# 부서별 결혼 비율
print(462.195238 / 498.804762,
30.3 / 32.7,
214.504762 / 231.495238)
> stats

결과해석
- 귀무가설 :부서별로 결혼 비율은같다.
- 결과 :p-value > 0.05 →귀무가설을 기각할 수 없음.
- 해석 :부서별 결혼 비율에 통계적으로 유의한 차이는 없다.
- cramer
:집단간의 차이가 얼마나 나는가 (range : 0 ~ 1)
1에 가까우면 부서에 따라 결혼의 여부가갈리는것
위 결과에서는 cramer가 0.03으로 매우 작으므로 부서와 결혼을 관련이 별로 없다.
예) 카이제곱 검정을 할 수 있는 경우
광고를 여러가지 버전으로 했을 때
A 집단은 광고를 보고 지나쳤고, B집단은 광고를 보고 들어왔다.
VER2 광고가 클릭이 좀더 높다면, 이것이 통계적으로 유의한 차이가 있을까?
'기초통계' 카테고리의 다른 글
| [기초통계] 상관과 회귀 : 상관분석, 상관계수, 상관과 인과 (0) | 2022.08.20 |
|---|---|
| [기초통계] 집단 비교 : 분산분석 - 다중비교, 사후검정, 카이제곱검정 (0) | 2022.08.19 |
| [기초통계] A/B 테스트 (0) | 2022.08.18 |
| [기초통계] 통계적 가설 검정 (0) | 2022.08.18 |
| 확률과 통계 II : 모집단, 표본 그리고 표집 (0) | 2022.08.16 |