상관과 회귀 : 상관분석
KEYWORD
상관계수
기울기
공분산
피어슨 적률 상관계수
스피어만 상관계수
켄달 상관계수
상관과 인과
• 제3 변인의 존재
• 이질적인 집단들의 합 (심슨의 역설)
• 극단치(outliers)
상관계수
두 변수의 연관성을 -1 ~ +1 범위의 수치로 나타낸 것
• 두 변수의 연관성을 파악하기 위해 사용
• 어휘력과 독해력의 관계
• 주가와 금 가격의 관계
• 엔진 성능과 고객만족도의 관계
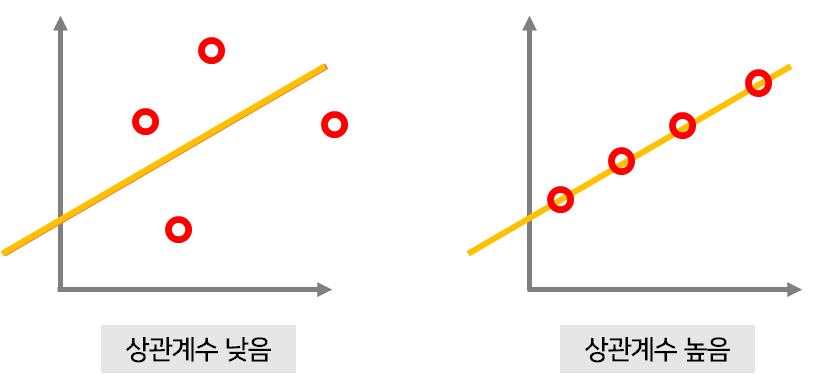
상관계수의 해석
부호와 크기
• 부호:
- + : 두 변수가 같은 방향으로 변화(하나가 증가하면 다른 하나도 증가)
- - : 두 변수가 반대 방향으로 변화(하나가 증가하면 다른 하나는 감소)
• 크기:
- 0 : 두 변수가 독립, 한 변수의 변화로 다른 변수의 변화를 예측하지 못함
- 1 : 한 변수의 변화와 다른 변수의 변화가 정확히 일치
기울기
기울기는 𝑦 = 𝑎𝑥 + 𝑏 에서 𝑎
𝑥가 1만큼 변할 때, 𝑦의 변화량을 나타냄
기울기가 클수록 𝑦가 크게 변함
* 상관계수와 다른 개념이므로 주의
상관계수
예) 일란성 쌍둥이의 키
공분산
X의 편차와 Y의 편차를 곱한 것의 평균 (X=Y이면 분산과 같음)

공(두 변수가 얼마나 같이 변하나?)
분산(한 변수가 얼마나 변하나)
· 공분산의 범위 : -∞ ~ +∞
우상향하는 추세인 경우 +로, 우하향하는 추세인 경우 - 로 커짐
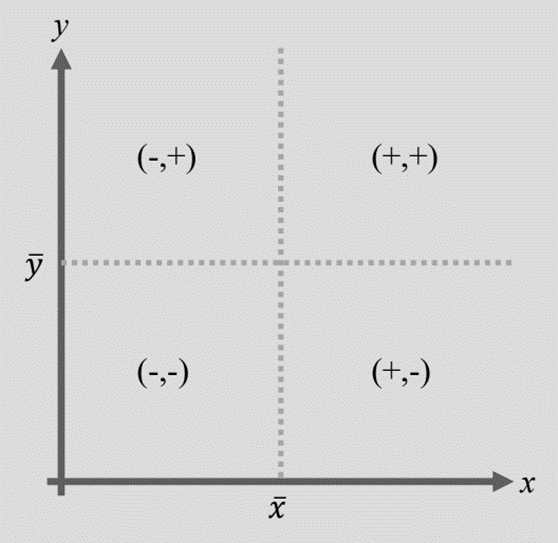
피어슨 적률 상관계수
가장 대표적인 상관계수

• 선형적인 상관계수를 측정
• 공분산을 두 변수의 표준편차로 나눔
- 범위 : -1 ~ +1
> 취약점 : 직선으로 우상향이면 상관계수가 높게 잡히는데 휘어지는 경우, 상향 추세여도 상관계수가 조금 떨어지게된다.
상관계수와 비단조적 관계
상관계수는 우상향 또는 우하향하는 단조적 관계를 표현
복잡한 비 단조적인 관계는 잘 나타내지 못함.
상관계수가 낮다고 해서 관계가 없는 것은 아니다.
> 상관계수가 '0'인 예시

상관분석 가설검정 순서도
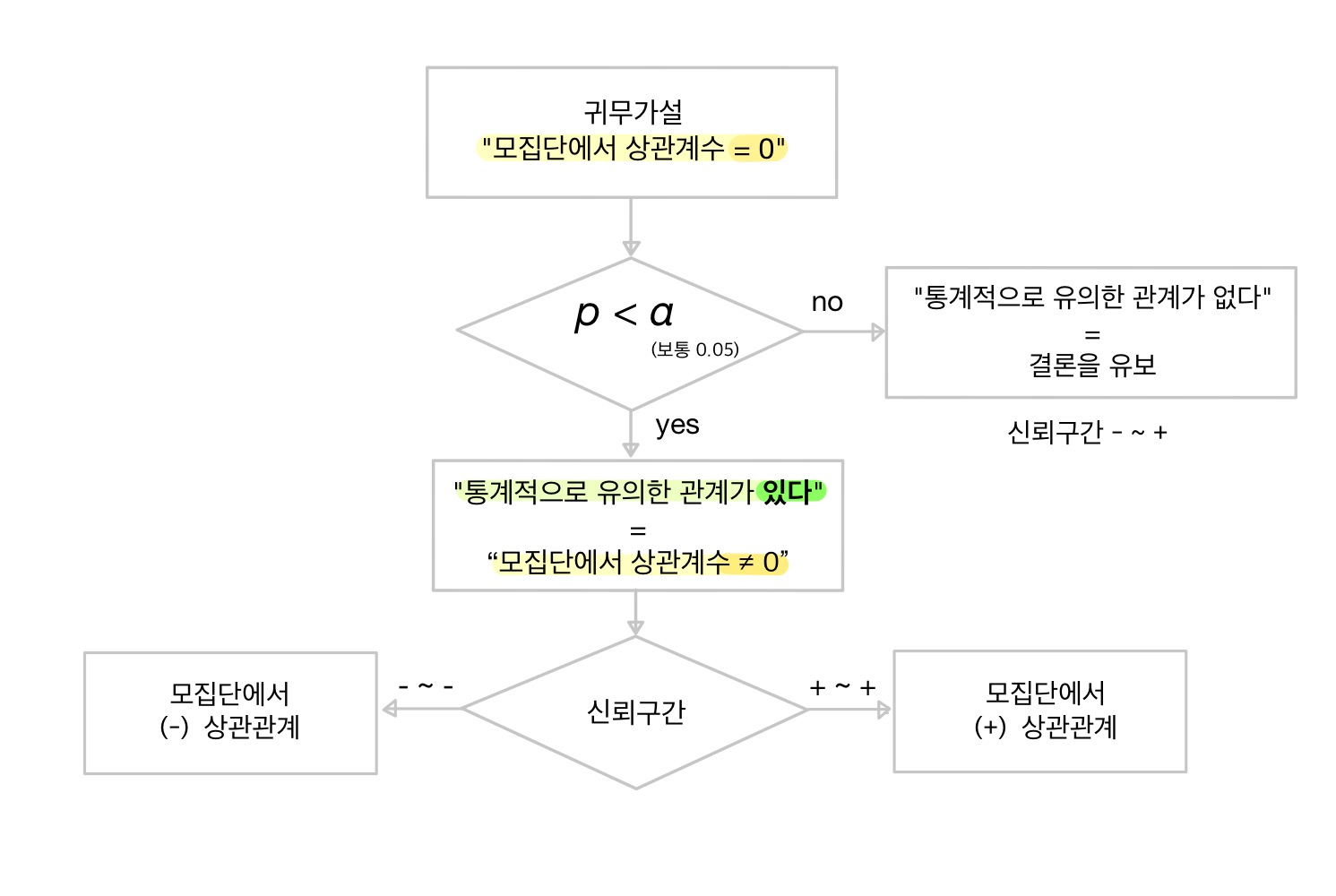
상관계수의 신뢰구간
| + ~ + | - ~ + | - ~ - |
| 모집단에서 두 변수의 관계가 + | 모집단에서 두 변수의 관계는 -, 0, + 모두 가능 |
모집단에서 두 변수의 관계가 - |
상관계수의 크기 해석
• 상관계수의 크기에 대해서는 몇 가지 권장 기준이 있지만
| 낮음 | 중간 | 높음 |
| ~0.1 | 0.1 ~ 0.5 | 0.5 ~ |
( 예: Cohen, 1988), 엄밀한 근거에 바탕을 둔 것은 아님.
• 실제 의사결정에서는 상대적으로 비교하는 것이 바람직하다.
예) 상관계수 0.2인 요소 A와 0.3인 요소 B가 있고, 예산상 한 가지 요소만 고려할 수 있다면 요소 B를 고려
피어슨 상관계수
Python
import pingouin as pg
pg.corr(x, y, alternative='two-sided', method='pearson', kwargs)
car = pd.read_excel('car.xlsx')
import pingouin as pg
pg.corr(car.price, car.mileage)
> 피어슨 상관계수 = -0.067616
> 상관계수의 신뢰구간 -0.74 - 0.61
(* 상관계수의 신뢰구간은 평균의 신뢰구간과 달리 좌우 대칭이 맞지 않는다.)
상관계수는 0 ~ 1 사이므로 상한선이 있어 좌우대칭이 맞지 않는다.
> 귀무가설 : 상관관계는 0 이다.
> p-val이 0.05보다 작으므로 귀무가설을 기각 → 통계적으로 유의한 상관관계가 있다.
● 예2) mileage(주행거리)와 other_car_dagame의 상관관계
import pingouin as pg
pg.corr(car.mileage, car.other_car_damage)
> 피어슨 상관계수 = 0.00795
> 상관계수의 신뢰구간 -0.11 ~ 0.13
> 귀무가설 : 상관관계는 0 이다.
> p-val이 0.05보다 크므로 귀무가설을 채택 → 통계적으로 유의한 상관관계가 없다.
스피어만 상관계수
: 실제 변수값 대신 그 서열을 사용하여 피어슨 상관계수를 계산
• 한 변수의 서열이 높아지면 다른 변수의 서열도 높아지는지를 나타냄
• 두 변수의 관계가 비선형적이나 단조적일 때 사용
Python
pg.corr(car.price, car.mileage, method='spearman')

켄달 상관계수
: 모든 사례를 짝지어 X의 대소관계와 Y의 대소관계가 일치하는지 확인

• 데이터가 작을 때 사용.
• 단점 : 모든 사례를 짝지어야 하므로 데이터가 많을 때는 비효율적이다.
Python
pg.corr(car.price, car.mileage, method='kendall')

> 스피어만과 켄달 상관계수는 p-val가 매우 작게 나왔다 → 상관계수가 유의하다.
결론 : 비선형적이지만 단조적인 관계는 어느정도 있다.
> 시각화
car.plot(x='mileage', y='other_car_damage', kind='scatter', color='orange')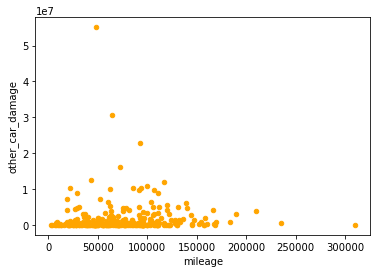
∴
비선형적인 관계가 있을 것으로 판단되면, 스피어만이나 켄달 상관계수를 구해보면 된다.
'스피어만'이나 '켄달'은 극단적인 수치가 서열로 정렬되기 때문에 값의 크기에 영향을 덜 받는 것이 강점이 될 수 있다.
'상관' 과 '인과' correlation and causation
두 변수의 상관관계는 인과관계를 담보하지 않으며,
상관관계가 있다고 반드시 인과관계가 있는 것은 아님
• 제3 변인의 존재
• 이질적인 집단들의 합 (심슨의 역설)
• 극단치(outliers)
제 3의 변인
두 변인이 상관관계처럼 보이더라도, 두 변인 모두에게 영향을 미치는 제 3변인이 있을 수 있기 때문에,
이러한 상관관계를 인과관계로 확정할 수 없음.
• '도시 내 범죄 발생 건수'와 '종교 시설의 수'는 양의 상관 관계가 있음
- 범죄가 많아서 종교에 의존하는가? 또는 종교가 범죄를 부추기는가?
- 사실은 인구가 많아지면 범죄도 늘고, 종교 시설도 많아짐
심슨의 역설
심슨의 역설은 데이터의 세부 그룹별로 일정한 추세나 경향성이 나타나지만, 전체적으로 보면 그 추세가 사라지거나
반대 방향의 경향성을 나타내는 현상 (이 현상은 사회과학이나 의학 통계 연구에서 종종 발생한다)
각 집단별 상관관계와 전체 총합의 상관관계는 다를 수 있음.
상관분석 결과가 예상과 다를 경우, 이질적인 하위집단들이 존재하는지 살펴 봐야 할 수도 있음
극단치 outlier
자료 내에 극단치가 있을 때,
• 존재하지 않는 상관관계가 나타나는 경우
• 존재하는 상관관계가 포착되지 못하는 경우
'기초통계' 카테고리의 다른 글
| 상관과 회귀 : 회귀분석 (0) | 2022.09.05 |
|---|---|
| [실습] 집단분석 : Depression.xlsx 데이터 (0) | 2022.08.25 |
| [기초통계] 집단 비교 : 분산분석 - 다중비교, 사후검정, 카이제곱검정 (0) | 2022.08.19 |
| [기초통계] 집단 비교 : 독립표본 t검정, 검정력, 효과크기, 분산분석, 분할표 (0) | 2022.08.18 |
| [기초통계] A/B 테스트 (0) | 2022.08.18 |