상관과 회귀 : 회귀분석
KEYWORD
지도학습
예측
회귀분석, 분류분석
잔차
최소제곱법
R제곱과 피어슨 상관계수
더미코딩
범주 설정하기
지도학습
독립변수 x를 이용해서 종속변수 y를 예측하는 것
| 독립변수 independent variable |
종속변수 dependent variable |
| 예측의 바탕이 되는 정보, 인과관계에서 원인, 입력값 | 예측의 대상, 인과관계에서 결과, 출력값 |
통계에서 '예측'이란?
어떤 값에 대한 추론을 의미함 (시간적인 의미는 아님)
지도학습에서 예측은 변수들 사이의 패턴을 파악해서 한 변수로 다른 변수를 추론하는 것
시계열 분석 등에서 하는 미래에 대한 예측은 forecasting.
종속변수에 따른 지도학습 구분
| 회귀분석 regression |
분류분석 classification |
| • 종속변수가 연속형 • (예측값 – 실제값) 으로 정확성을 계산 예) 가격, 크기, 선호도 예측 |
• 종속변수가 범주형 • 예측의 정확성을 다른 방식으로 계산 |
선형 모형

• 𝑦^ : 𝑦의 예측치
• 𝑥 : 독립변수
• 𝑤 : 가중치 또는 기울기
• 𝑏 : 절편(𝑥 = 0 일 때, y의 예측치)
회귀분석 예시
> 피부암 사망률
독립변수(x) : 위도
종속변수(y) : 천만명당 사망자 수

> 적도(x=0)에서는 1000만명당 389.2명이 사망할 것으로 예측된다.
잔차 residual
: 실제값(y) 과 예측값(y^) 의 차이
· 잔차분산 : 잔차를 제곱해서 평균을 낸 것
cf. 분산 : 편차 (실제값과 평균의 차이) 제곱의 평균
| 잔차분산이 크다 → 예측이 잘 맞지 않음 잔차분산이 작다 → 예측이 잘 맞음 |
최소제곱법 Ordinary Least Squares
: 잔차 분산이 최소가 되게 하는 w, b등 계수를 추정
가장 널리 사용되는 추정방법으로
분산의 계산에 제곱이 들어가므로 최소'제곱'법이라고 한다.
Python 에서 '회귀분석'
from statsmodels.formula.api import ols
> 분석 및 결과
종속변수(y) 와 독립변수(x) 의 형식으로 관계식을 표현
m = ols('종속변수(y) ~ 독립변수(x)', data = '데이터 ').fit()
m .summary()
from statsmodels.formula.api import ols
# 분석
m = ols('price ~ mileage', date = df).fit()
# 결과
m.summary()회귀계수 추정 결과
price = −0.052 × mileage + 1258.7668
| 추정치 표준오차 검정통계량 p-value 신뢰구간 | |
절편 mileage의 기울기 |
 |
표준오차와 검정통계량은 p-value를 구하기 위한 것이므로 직접 해석할 필요가 없다.
p-value > (귀무가설) 절편이 0이다.
(귀무가설) 기울기가 0이다.
→ 기울기 신뢰구간이 -0.006 ~ -0.005 이므로 p-value는 볼 필요가 없다.
회귀계수 가설 검정
귀무가설 : 모집단에서 회귀계수 = 0
| 가설검정 | 신뢰구간 |
| 유의하지 않음 | - ~ + |
| 유의함 (p < α ) | - ~ - 또는 + ~ + |
예측
새로운 데이터 만들기
모형에 입력해서 예측하기 m.predict( )
import pandas as pd
from statsmodels.formula.api import ols
df = pd.read_excel("car.xlsx")
m = ols('price ~ mileage', df).fit() # 회귀분석
m.summary()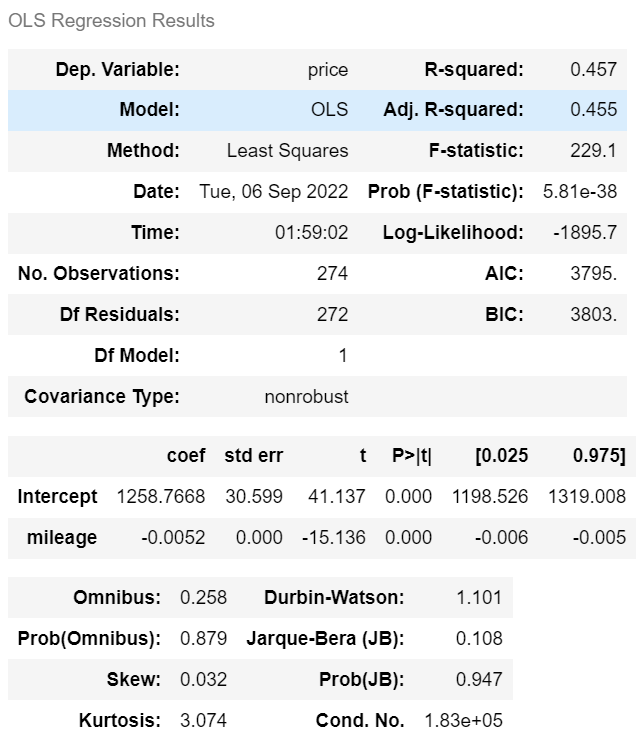
> R-squared : 주행거리가 분산의 45.7% 를 설명한다.
m = ols('price ~ mileage', df).fit() # 회귀분석
# 새로운 데이터 만들기
new_df = pd.DataFrame({'mileage':[10000, 20000]})
# 모형에 입력하여 예측하기
m.predict(new_df)> 모델 예측에 따라 price 예측값이 나오게 된다.

import seaborn as sns
sns.regplot(x='mileage', y ='price', data=df)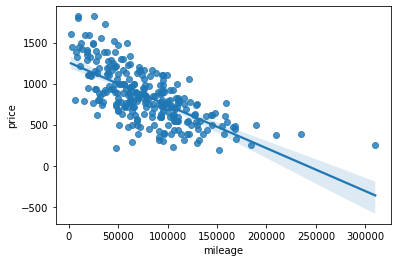
m2 = ols('price ~ other_car_damage', df).fit()
m2.summary()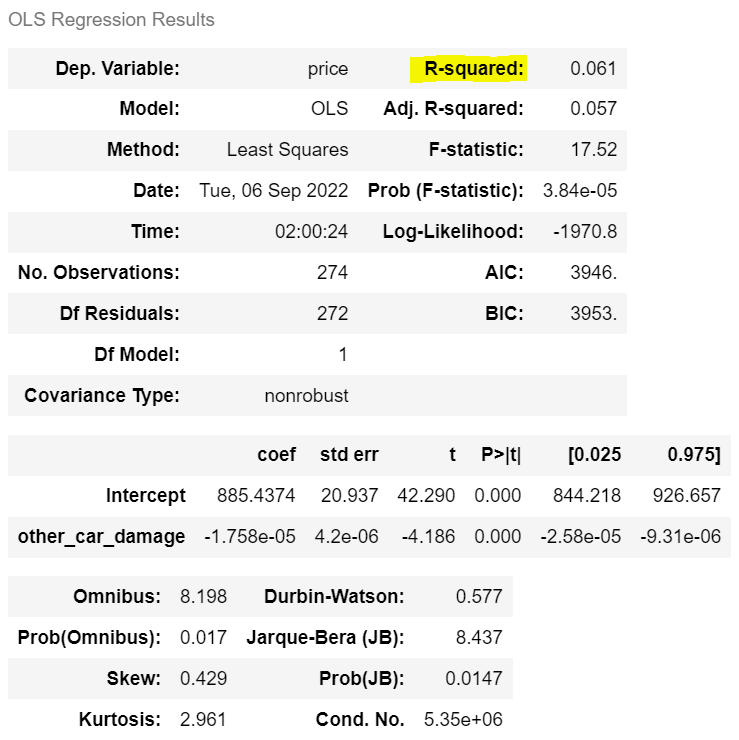
R 제곱 R sqaured
회귀 분석에서 예측의 정확성을 알기 쉽게 판단할 수 있게 만든 지표 (0~1)

해석하기 >
| 0 | 분석결과가 y의 예측에 도움이 안됨 |
| 1 | y를 완벽하게 정확히 예측할 수 있음 |
· R²이 0이 되는 경우?
(잔차분산 / 분산 ) = 1 일때,
즉 잔차분산 = 분산
이것은 (실제값-예측값) = (실제값-평균)
> 평균으로 밖에 예측하지 못할 때, 잔차분산이 분산과 같아진다.
< R제곱 읽는 법 >
"모형이 종속변수의 분산의 ~% 를 설명한다"
예: R제곱 = 0.3 → "분산의 30%를 설명한다"
• R제곱은 TSS(분산)에 비해 RSS가 얼마나 작아졌는지를 나타냄
• TSS와 RSS는 모두 평균, 또는 예측에 대한 변산성(불확실성)
• 변산성이 줄어들었다 → 불확실성이 줄어들었다 → 설명이 되었다.
> R 제곱이 너무 낮게 나오면 다른 변수로 분산을 해보는 것이 좋다.
R제곱과 피어슨 상관계수
단순회귀분석(독립변수가 1개인 회귀분석)의 경우
회귀분석의 R제곱 = 독립변수와 종속변수의 피어슨 상관계수의 제곱
예시) 자동차 마일리지와 가격의 상관계수
import pandas as pd
import pingouin as pg
car = pd.read_excel('car.xlsx')
pg.corr(car.mileage, car.price)
(-0.67616)² = 0.4571923456
● 독립변수가 ' 범주형 '인 경우
예) 독립변수가 '차종' 일 경우 가격 예측
from statsmodels.formula.api import ols
m_model = ols('price ~ model', data=car).fit()
m_model.summary()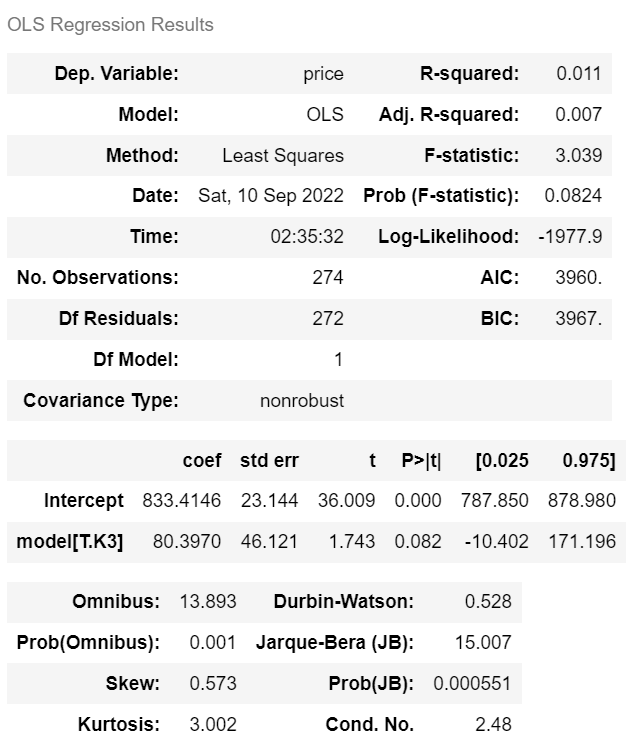
범주형 변수는 기울기를 곱할 수 없다.
연속 변수로 변환해서 모형에 투입 한다.
여러가지 방법이 있는데 가장 많이 사용하는 것은 더미코딩(Jamovi, R, Pythom은 자동으로 가능)
더미코딩 Dummy coding
범주형 변수에 범주가 k개 있을 경우 (k-1)개의 더미 변수를 대신 투입
• 범주 중에 하나를 기준 범주로 지정
- 기본적으로 ABC 순으로 먼저 나오는 것이 기준 범주 (변경 가능)
• 기준 범주를 제외한 범주들은 범주별로 더미 변수를 하나씩 가짐
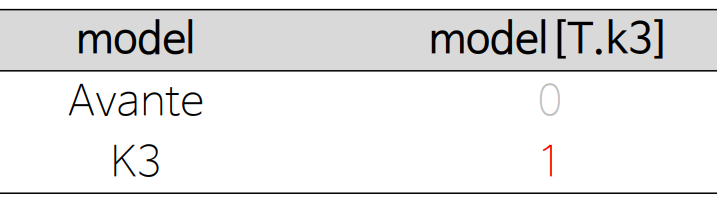
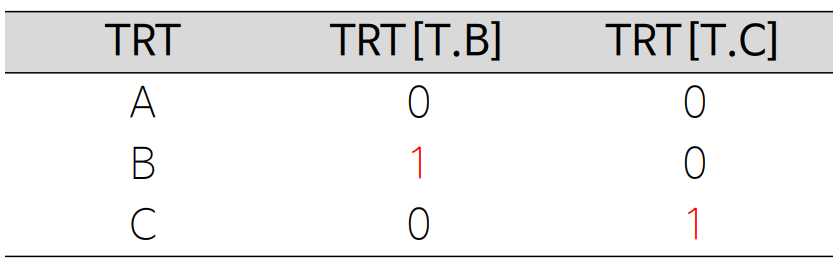
| 범주가 2개 인 경우 | 범주가 3개 인 경우 |
| ols('price ~ model', df).fit().summary() | dep = pd.read_excel('depression.xlsx') ols('y ~ TRT', dep).fit().summary() |
 |
 |
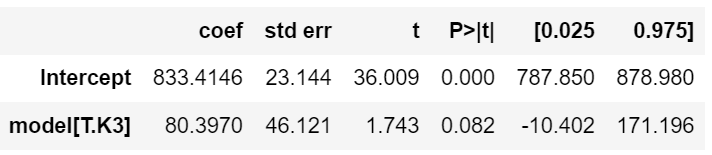
| • ABC 순으로 Avante가 기준 - K3의 더미 변수 추가 - 0 = No, 1 = Yes로 이해 |
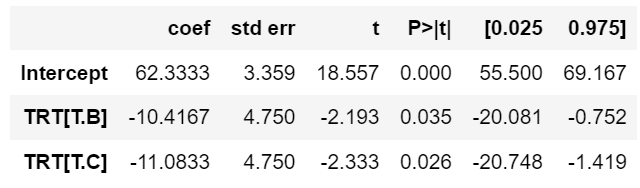
• ABC 순으로 A가 기준 • B와 C의 더미 변수 추가 • 0 = No, 1 = Yes로 이해 |
 |
 |
 |
 |
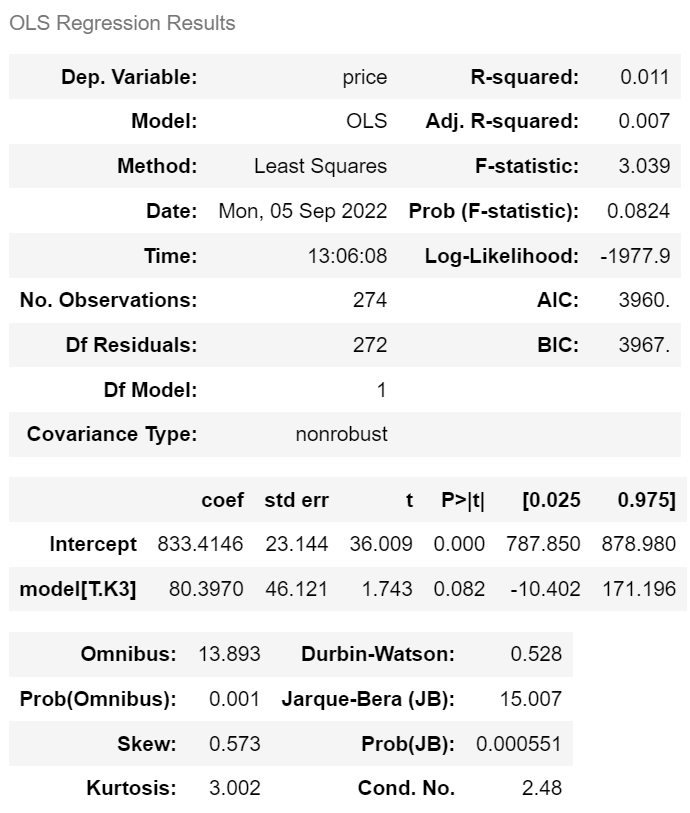
| • Avante 예상 가격: 833만원 • K3 예상 가격: 833+80 =913만원 |
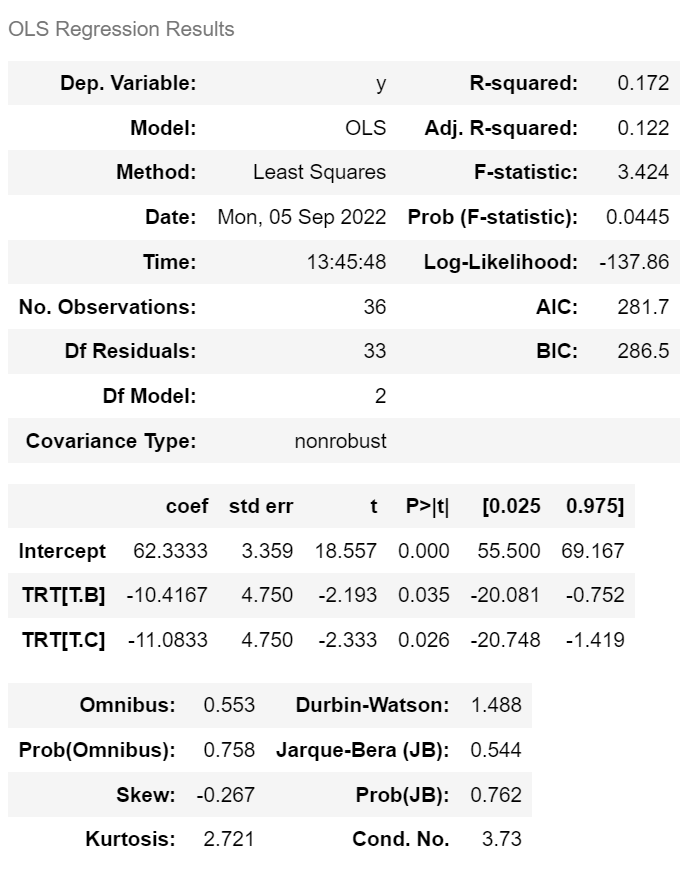
• A(기준)의 치료효과 : 62.3333 • B의 치료효과: 62.3333 – 10.4167 = 51.9166 • C의 치료효과: 62.3333 – 11.0833 = 51.2500 |
| p-val = 0.082로 0.05보다 큼 즉 귀무가설을 기각할 수 없다. 'k3가 Avante와 가격이 차이가 없다'를 기각 못함 |
> 예측에서 신뢰구간은 사용하지 않는다.
선형 회귀분석과 분산분석
'분산 분석'은 선형 회귀분석의 특수한 경우,
| 분산 분석은 · 서로 다른 두 개의 선형회귀분석의 성능 비교에 응용할 수 있으며 · 독립변수가 카테고리 변수인 경우 각 카테고리 값에 따른 영향을 정량적으로 분석하는데도 사용된다. |
> 선형 회귀 분석의 F 검정과 그 p 값을 보면, 분산분석과 같다.
pg.anova(dep, dv='y', between='TRT')
범주 목록 보기
기준 범주는 분석 전에 정해야 한다.
unique 함수를 사용하면 변수에서 범주의 목록을 확인 할 수 있다.
기준 범주는 더미 변수가 없으므로, 범주 목록에서 확인한다.
Python 에서 더미변수 다루기
• 변수 model을 명시적으로 범주형 변수로 지정하기
(변수가 수치형인 경우에만 필요)
ols('price ~ C(model)', car).fit().summary()
• 변수 model의 기준 범주를 K3로 지정하기
ols(' price ~ C(x, Treatment("K3"))', car).fit().summary()
ols('price ~ C(model, Treatment("K3"))', car).fit().summary()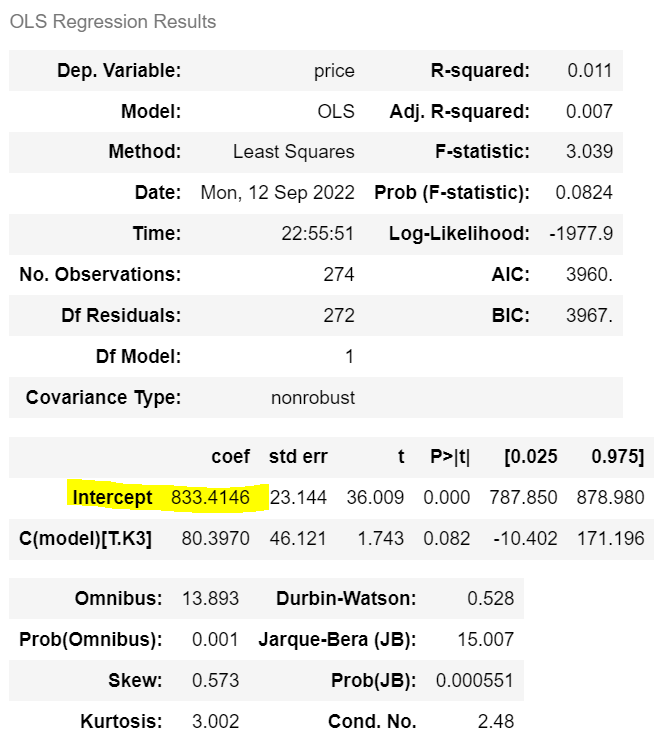 |
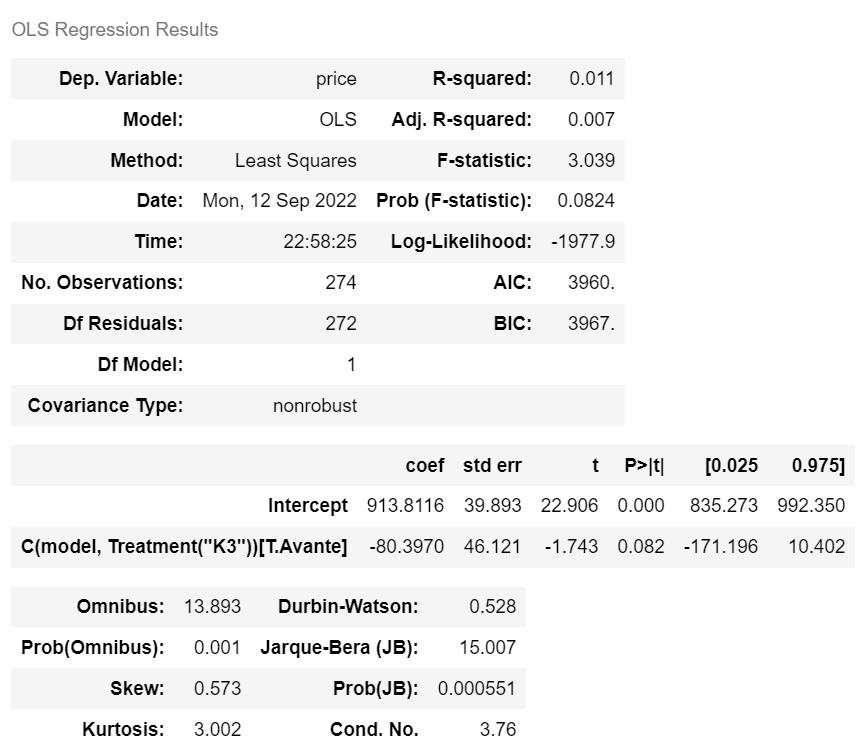 > 기준이 K3로 바뀐것을 볼 수 있다. ( intercept = 913.8116) |
기준 범주 바꿔주기
• [dep 데이터/ 종속변수 3개] 변수 model의 기준 범주를 'C'로 지정하기
ols(' price ~ C(x, Treatment("C"))', dep).fit().summary()
# 범주가 세개일때
from statsmodels.formula.api import ols
import pandas as pd
dep = pd.read_excel("depression.xlsx")
m = ols('y ~ C(TRT, Treatment("C"))', dep).fit()
m.summary()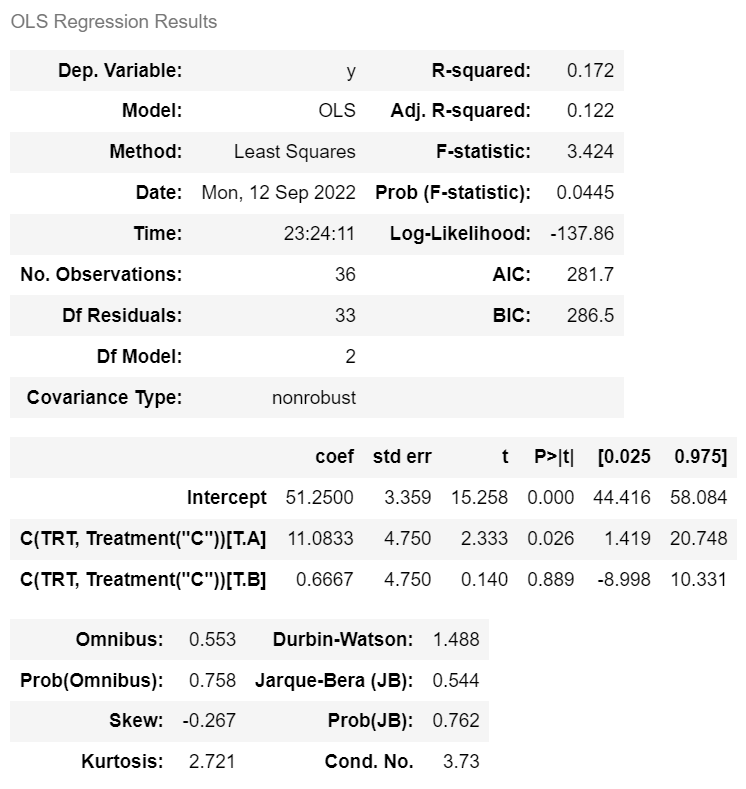
'기초통계' 카테고리의 다른 글
| 다중회귀분석 : 교차검증 (0) | 2022.09.06 |
|---|---|
| 회귀분석 : 다중회귀분석 (0) | 2022.09.05 |
| [실습] 집단분석 : Depression.xlsx 데이터 (0) | 2022.08.25 |
| [기초통계] 상관과 회귀 : 상관분석, 상관계수, 상관과 인과 (0) | 2022.08.20 |
| [기초통계] 집단 비교 : 분산분석 - 다중비교, 사후검정, 카이제곱검정 (0) | 2022.08.19 |