상관과 회귀 : 다중회귀분석
KEYWORD
다중회귀분석
통계적 통제
표준화
모형선택
과적합
AIC, BIC
다중회귀분석
독립변수가 2개 이상인 회귀분석
Python에서는 관계식에서 +로 변수를 구분
예)
'price ~ mileage + model'
from statsmodels.formula.api import ols
m = ols('price ~ mileage + model' , df).fit()
m.summary()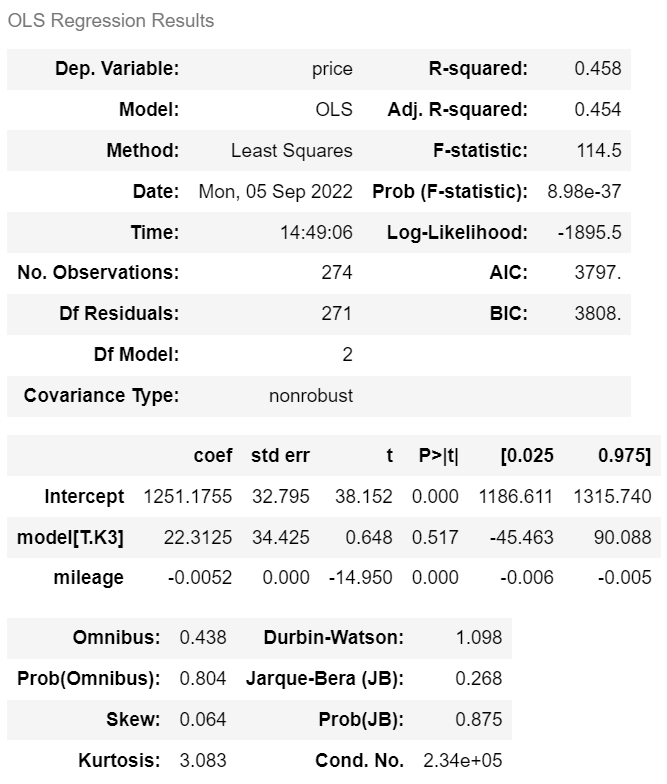
price = (-0.0052 × mileage) + (22.3125 x model) + 1251.1755
> 'K3'라면 model에 1 대입
다중회귀 분석을 하는 이유
22만원 차이는 주행거리를 통제했을 때의 차이인 것이다.
단순히 k3와 아반떼의 가격비교 질문을 받으면 k3와 avante의 가격만 비교하면 된다.
'price ~ model'
그런데 만약 k3가 아반떼보다 왜 더 비싸냐? 라는 질문을 받으면
'price ~ model + mileage'
주행거리를 통제해서 시장에 k3는 신차가 더 많이 나와있고 아반떼는 탄 차들이 많이 나와서 그렇다고 답할 수 있다.
즉, 질문에 따라 필요하다면 다중회귀분석을 통해서 질문의 요지에 맞게 더 상세한 답을 할 수 있다.
| from statsmodels.formula.api import ols m_mileage = ols('price ~ mileage' , df).fit() m_mileage.summary() |
from statsmodels.formula.api import ols m_year = ols('price ~ year' , df).fit() m_year.summary() |
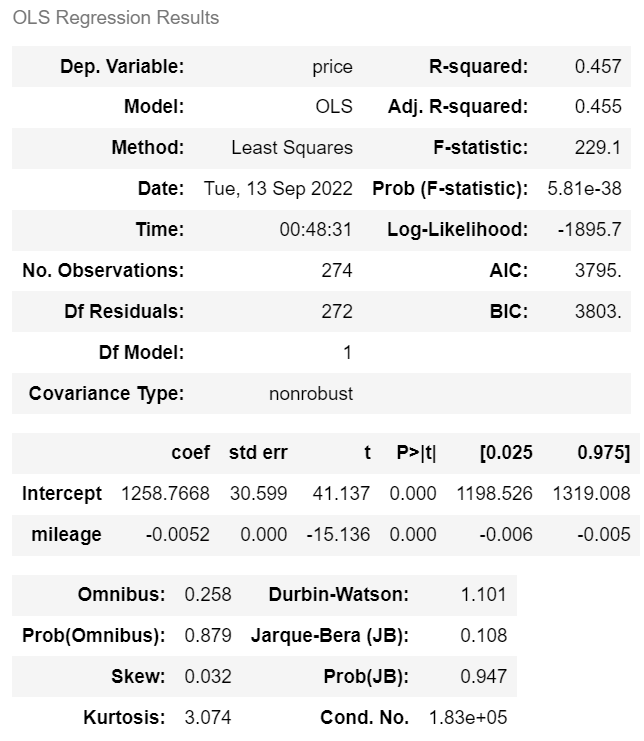 |
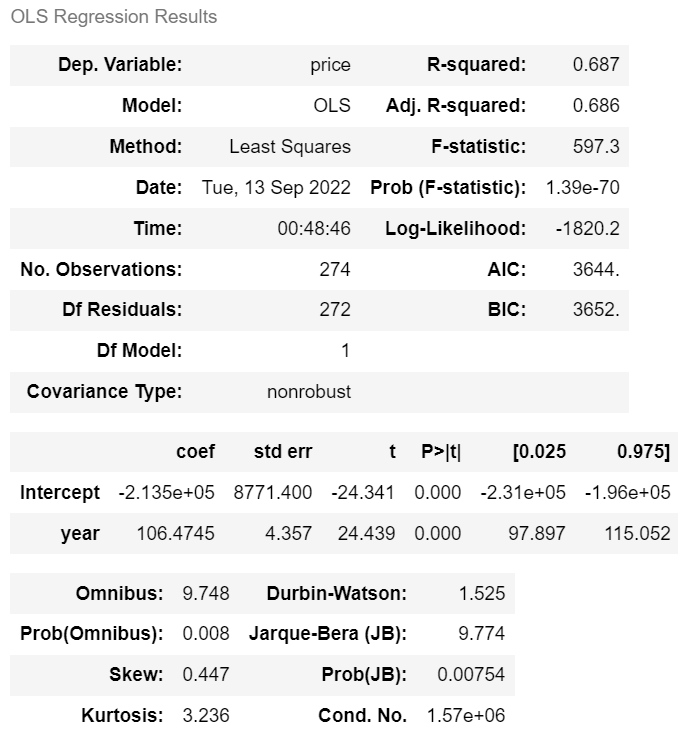 |
| from statsmodels.formula.api import ols m3 = ols('price ~ mileage + year' , df).fit() m.summary() |
|
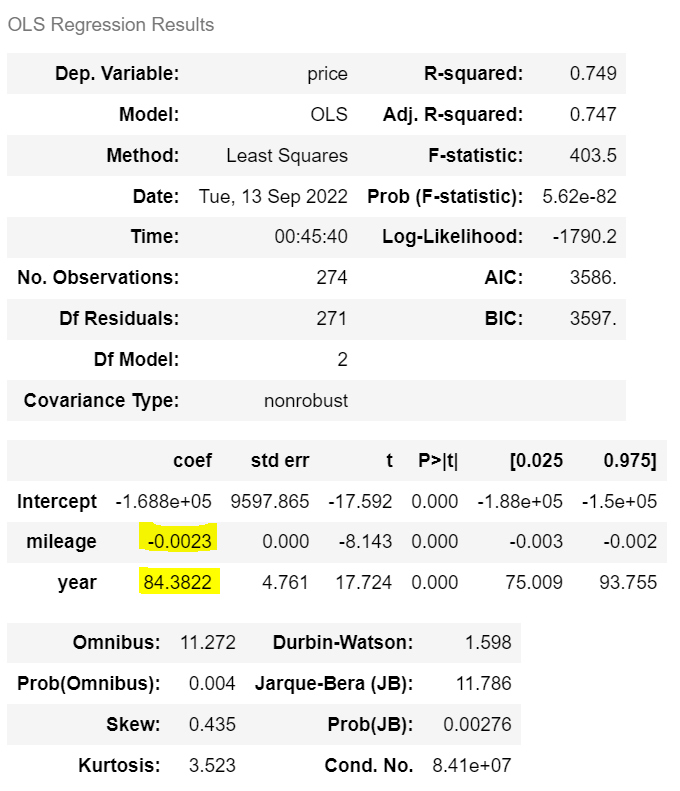 |
|
통계적 통제
독립변수 x와 상관관계가 높은 요소 z가 존재할 경우
z가 종속변수 y에 미치는 영향이 x의 기울기에 간접 반영될 수 있음.
• 실험적 통제
: 데이터에서 z를 일정하게 유지하여, z의 영향을 제거
• 통계적 통제
: z를 모형에 독립변수로 함께 포함하여, x의 기울기에 z의 영향이 간접 반영되지 않도록 함.
예)
사람이 흡연을 해서 폐암에 걸리는게 아니고
스트레스를 많이 받는 사람은 폐암에 잘걸리는데 스트레스를 많이 받는 사람이 흡연을 많이해서
흡연을 많이 하는 사람이 폐암에 걸리는 것이다 라는 주장
스트레스, 흡연도 변수에 넣고 폐암에 걸리는가?
회귀분석을 해본다.
스트레스 때문에 폐암에 걸리는 것이라면 흡연과 폐암의 관계는 없어지는 것
그러나 흡연과 폐암은 실험적 통제가 어렵다.
흡연이 폐암에 미치는 영향을 알아보려고 30년 흡연을 권할 수는 없지 않은가?
표준화 standardization
다중회귀분석에서 독립변수는 단위가 다르므로 종속변수에 대한 영향력을 비교하기 어려움
(X - 평균) / 표준편차
• 표준화를 하면 평균 = 0, 표준편차 = 1이 됨
• 표준화를 통해 변수의 '단위'를 제거하여 상대적인 영향력을 비교할 수 있음
연습
'종속변수 ~ scale(독립변수)'
from statsmodels.formula.api import ols
m_scale = ols('price ~ scale(mileage) + scale(year)', df).fit()
m_scale.summary()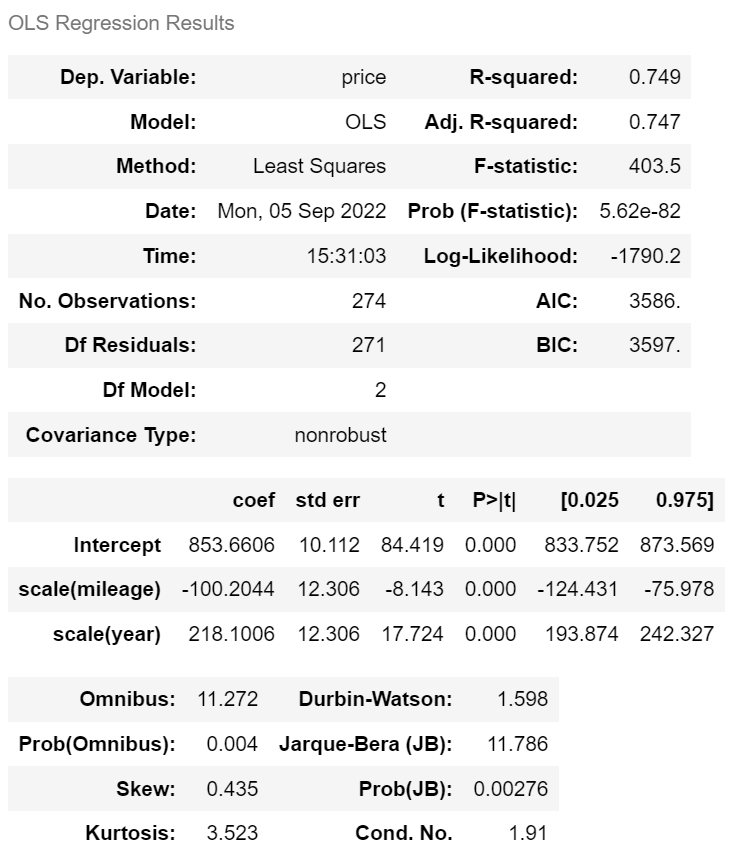
> 표준화 전
mileage 가 1km마다 -0.0023
year 가 1년마다 + 84
> 표준화 후
표준화된 마일리지에 대해서는 기울기가 -100, 표준화된 연식에 대해서는 기울기가 218
mileage 가 1표준편차마다 -100만원
year 이 1표준편차마다 +218만원
∴ 표준화를 해보니 연식(year)이 주행거리(mileage)보다 중고차 가격에 영향이 더 큰 것을 알 수 있다.
(표준화로 환산된 값을 기준으로 기울기를 비교하는 것)
모형 선택
다중회귀 분석을 하면 통계적 분석이 되므로 엄격하게 분석이 가능하다.
그런데 최소제곱법을 사용해서 잔차가 작은 쪽으로 예측을 하게 된다.
다중회귀분석에서 복잡한 분석은 단순한 분석보다 R²이 무조건 높다..
이럴 때 좋은 예측 모형을 만들기 위한 독립 변수는 어떻게 선택할 수 있을까?
과적합
최소제곱법은 RSS가 가장 작은 계수를 추정
• 주어진 표본에 가장 맞는 계수를 찾게 됨.
• 표집 오차가 존재하기 때문에, 주어진 표본에 지나치게 맞는데 계수를 추정하면 모집단의 계수와 다를 수 있음
독립변수의 개수와 과 적합
최소제곱법은 RSS가 작아지는 방향으로 계수를 추정함.
• 종속변수와 아무 관련이 없는 독립변수를 추가하더라도 RSS가 커지는 경우는 없음
• 모집단에서는 아무 관련이 없어도 표본에서는 약간의 관계라도 있을 수 있으므로 RSS는 작아지게 됨
• 독립변수가 많으면 많을수록, RSS는 무조건 ▼ (R제곱은 ▲)
수정 R 제곱과 AIC, BIC
여러 모형을 비교할 때 R제곱을 사용하면 독립변수가 많은 모형에 편향
독립변수의 개수를 이론적으로 보정한 수정 R제곱, AIC, BIC 등 지수가 있음.
• 수정 R제곱 : R제곱을 보정 → 클수록 좋음.
• AIC와 BIC : RSS(잔차분산)를 보정 → 작을수록 좋음.
∴ 수정된 R², AIC, BIC를 보면 독립변수로 선택할 지 말지를 고려할 수 있다.
연습 1
| ● 중고차 데이터 독립변수에 따른 가격 예측 : 적합한 독립변수 고르기 | |
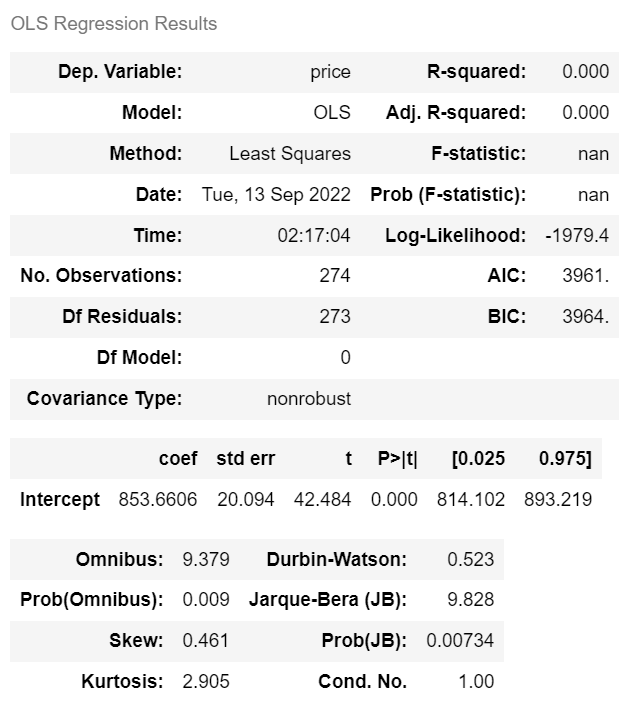
| from statsmodels.formula.api import ols ols('price ~ 1', df).fit().summary() |
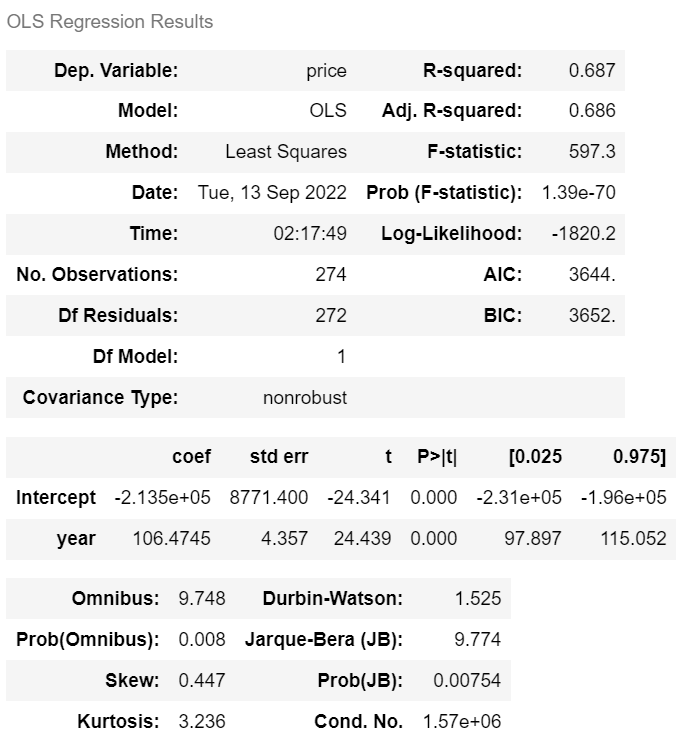
ols('price ~ year', df).fit().summary() |
 |
 |
| · 수정된 R² = 0.000 · AIC = 3961. · BIC = 3964. |
· 수정된 R² = 0.686 · AIC = 3644. · BIC = 3652. |
ols('price ~ year + mileage', df).fit().summary() |
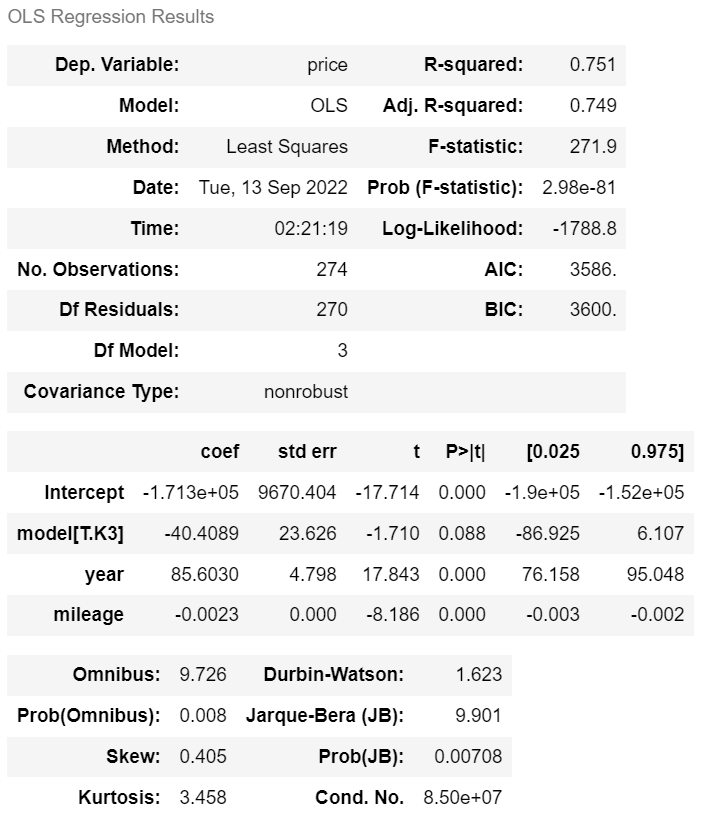
ols('price ~ year + mileage + model', df).fit().summary() |
 |
 |
| · 수정된 R² = 0.747 · AIC = 3586. · BIC = 3597. |
· 수정된 R² = 0.749 · AIC = 3586. · BIC = 3600. |
| > 변수 model은 예측에 도움이 되는지 약간 애매하다는 것을 알 수 있다. | |
> 수정된 R², AIC, BIC를 고려하면서 나중에 데이터 분석 예측에 대한 결과까지 보면서 적합한 지수를 선택해서 사용하는 것이 좋다.
연습 2
| ● 신생아 무게에 영향을 미치는 산모의 흡연, 임신기간 | |
| import pandas as pd from statsmodels.formula.api import ols bs = pd.read_excel("birthsmokers.xlsx") ols('Wgt ~ Smoke', bs).fit().summary() |
ols('Wgt ~ Gest', bs).fit().summary() |
 |
 |
| · 수정된 R² = 0.018 · AIC = 467.6 · BIC = 470.5 |
· 수정된 R² = 0.768 · AIC = 420.4 · BIC = 423.4 |
| ols('Wgt ~ Smoke + Gest', bs).fit().summary() | |
 |
> 결과를 보면 독립변수 추가에 따라 R²이 증가하고 AIC, BIC 작아진다. 그런데 여기서 p-val만 고려하게 되면 변수가 통계적으로 유의미한 의미가 없다고 판단되어 제거해버릴 수 있다. 따라서 여러가지 변수를 고려하게 될 때에는 p-val에 집착하지 않고 지수를 보면서 판단하는 것이 현명하다. |
| · 수정된 R² = 0.889 · AIC = 397.6 · BIC = 402.0 |
|
bs.groupby('Smoke').agg('mean')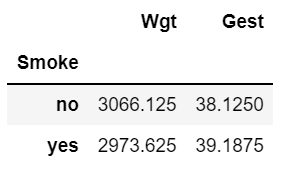
import seaborn as sns
sns.lmplot(x='Gest', y='Wgt', hue='Smoke', data=bs)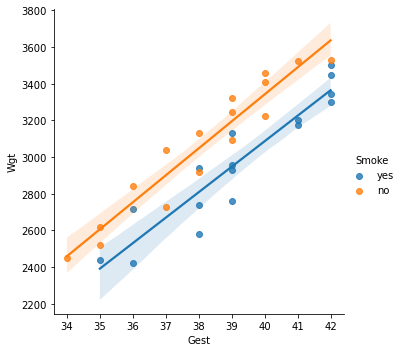
'기초통계' 카테고리의 다른 글
| 다중회귀분석 : 단계적 회귀분석 (0) | 2022.09.06 |
|---|---|
| 다중회귀분석 : 교차검증 (0) | 2022.09.06 |
| 상관과 회귀 : 회귀분석 (0) | 2022.09.05 |
| [실습] 집단분석 : Depression.xlsx 데이터 (0) | 2022.08.25 |
| [기초통계] 상관과 회귀 : 상관분석, 상관계수, 상관과 인과 (0) | 2022.08.20 |