변수의 변형
KEYWORD
변수의 변형
로그 함수
왜도
회귀분석과 산점도
I함수
절편이 없는 모형
절편 이동
변수의 변형
선형 모형은 독립변수와 종속변수의 선형적 관계를 가정한다는 한계
• 독립변수를 비선형 변환하면 이 한계를 일부 극복할 수 있음.

• Python은 관계식에 수학 함수를 사용하면 자동으로 변수 변환
로그함수
오른쪽 위로 갈수록 완만해지는 형태
• 가로축에서 1, 10, 100이 세로축에서 같은 간격(예: 0, 1, 2)
• 데이터에 적용하면 오른쪽을 왼쪽으로 끌어당기는 효과
- 일반함수 눈금 : 1 2 3 4 5 ... - 로그함수 눈금 : 1 10 100 1000 10000 ...
• 독립변수에 오른쪽으로 크게 떨어져 있는 값이 있는 경우, 로그 함수를 적용해주면 간격을 일정하게 만들어 줄 수 있다
예) 소득
효과 > 위나 옆으로 늘어지는 형태의 곡선이 있을 때,
이 곡선을 잡아당겨서 직선 형태로 만들어주는 기능
| ● 중고차 데이터 |
|
import seaborn as sns import numpy as np sns.regplot(x=df.mileage, y=df.price) |
# 로그 함수를 사용했을 때 import seaborn as sns import numpy as np sns.regplot(x=np.log(df.mileage), y=df.price) |
 |
 |
| > log를 씌우면 2.71의 배로 넘어가면서 우측에 치우쳐져 있는 데이터를 끌어당겨오는 효과를 보인다. | |
| # 비선형으로 휘어진 데이터의 경우에 로그함수를 사용하면 데이터 분석을 더 잘할 수 있다. | |
| ols('price ~ mileage', df).fit().summary() | ols('price ~ np.log(mileage)', df).fit().summary() |
 |
 |
| > 로그 변환을 하면서 R² 이 증가하고 AIC, BIC가 낮아진 것을 확인할 수 있다. | |
Bending the Curve
Logarithmic scales can emphasize the rate of change in a way that linear scales do not. Italy seems to be slowing the coronavirus infection rate, while the number of cases in the United States continues to double every few days.

Q. 만약 어떤 사람이 로그함수로 데이터를 보정해서 분석하는 것에 감명을 받아서 적절치 않게 해당 방법을 썼다면,
그 오류를 잡아낼 수 있는 방법이 있을까요?
( 즉, 로그함수를 활용한 분석법을 잘 썼다고 판단할 어떤 기준이라던지가 있을까요?)
> 교차검증을 해보면 된다.
| ▶ 로그 함수 적용 | |
| from statsmodels.formula.api import ols m = ols('price ~ mileage', train_df).fit() y_pred = m.predict(test_df) # 예측값 mean_squared_error(test_df.price, y_pred) # 평균제곱오차 |
import numpy as np m_log = ols('price ~ np.log(mileage)', train_df).fit() y_pred = m_log.predict(test_df) mean_squared_error(test_df.price, y_pred) |
> 로그함수로 데이터를 보정해서 분석한 것이 오차가 훨씬 작다 (= 로그함수로 보정하길 잘했다.)
∴ 시간이 지날수록 늘어지는 것들에 대해서는 로그함수를 적용하면 되고
로그 함수의 적용이 애매하다고 느껴지면 교차검증을 통해 확인해보자.
왜도 skewness
데이터가 한쪽 방향으로 치우친 정도(해당 방향으로 극단치가 존재함.)

• Negative skew : - 방향으로 치우침
• Positive skew : + 방향으로 치우침
| 0 | ±0.5 | ± 1 |
| 좌우대칭 | 중간정도 치우침 | 극단적 치우침 |
Python에서의 왜도
from scipy.stats import skew
skew()
# 중고차 주행거리 분포
import pandas as pd
car = pd.read_excel('car.xlsx')
import seaborn as sns
sns.histplot(car['mileage'], color='orange', edgecolor='k')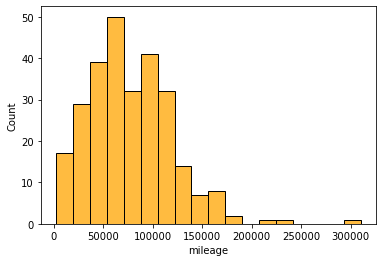
# 왜도
from scipy.stats import skew
skew(car['mileage'])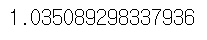
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
sns.histplot(np.log(car['mileage']), color='orange', edgecolor='k')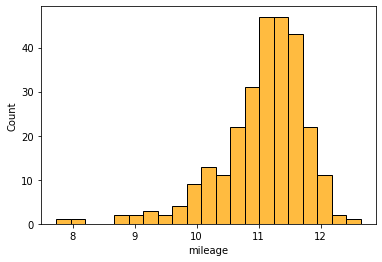
from scipy.stats import skew
skew(np.log(car['mileage']))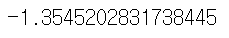
> 좌우대칭을 맞추고 싶다면 boxcox 를 활용한다.
from scipy.stats import boxcox
# boxcox
from scipy.stats import boxcox
x=boxcox(df.mileage)[0]
sns.histplot(x=x, color='green', edgecolor='k')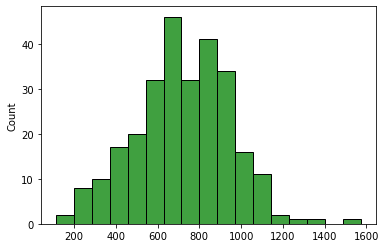
■ 표준화(Scale)와 로그변환(log)
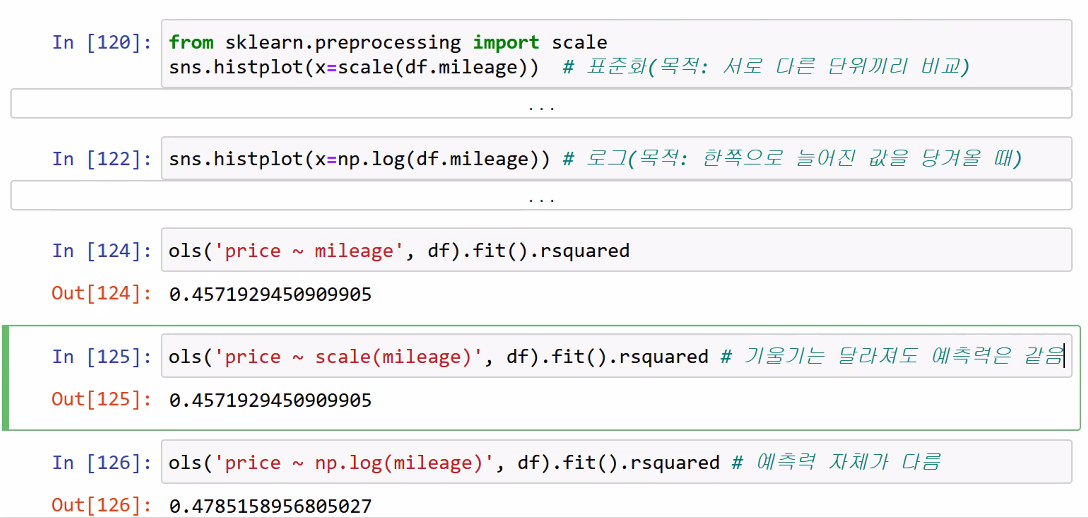
> 표준화는 기울기가 달라져도 예측력은 같지만, 로그 변환은 값이 달라지므로 예측력이 달라진다.
회귀분석과 산점도
| ▶ 로그 함수 적용 | |
| from statsmodels.formula.api import ols import matplotlib.pyplot as plt import pandas as pd car = pd.read_excel('car.xlsx') m = ols('price ~ mileage', car).fit # 회귀분석 plt.plot(car.mileage, car.price, 'o', color='green') # 산점도 |
from statsmodels.formula.api import ols import pandas as pd import numpy as np car = pd.read_excel('car.xlsx') m = ols('price ~ np.log(mileage)', car).fit plt.plot(np.log(car.mileage), car.price, 'o', color='green') |
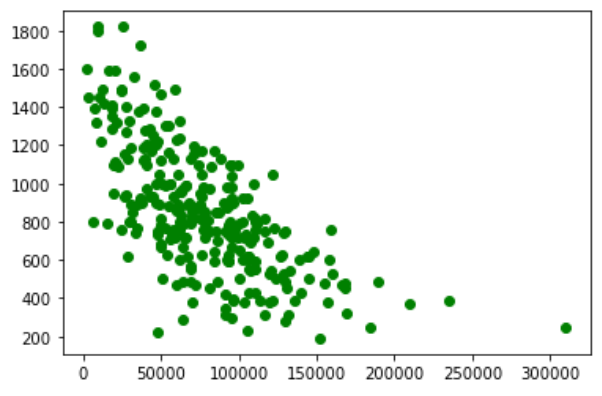 |
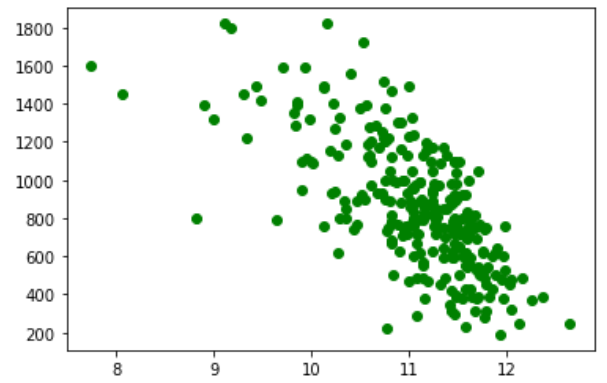 |
I함수
관계식에서 덧셈, 곱셈, 거듭제곱 등 할 경우 적용 불가한데
R과 Python은 I함수를 사용해서 계산을 적용 가능함.
y ~ I(x + z)
> 독립변수들을 더해서 회귀분석해라 라는 의미
즉, 독립변수 간에 원하는 계산을 해줄 수 있다.
독립변수 간 단위하고는 관련이 없다. 내가 독립변수간 하고 싶은 계산이 있을 때 사용하면 된다.
예) 속도 = 거리 / 시간
- 변수에서 주거리와 시간은 있는데 속도변수를 독립변수로 넣어주고 싶을 때
| ▶ I함수 적용해서 두 독립변수 더하기 | |
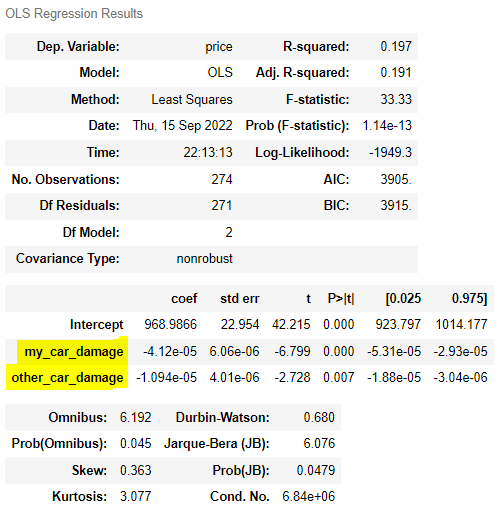
| from statsmodels.formula.api import ols ols('price ~ my_car_damage + other_car_damage', df) .fit().summary() |
from statsmodels.formula.api import ols ols('price ~ I(my_car_damage + other_car_damage)', df) .fit().summary() |
 |
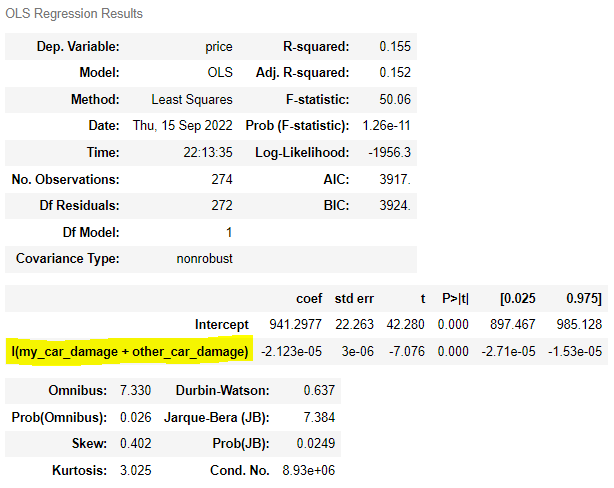 |
| > 다만, 이 경우에는 독립변수로 따로 회귀분석 하는 것이 I함수를 적용하는 것보다 수정된 R계수, AIC, BIC 지수가 더 낮았다. |
|
2차항의 추가
𝑦 = 𝑤2𝑥 2 + 𝑤1𝑥 + 𝑏와 같은 모형을 관계식으로 만들 경우
| R (거듭제곱에 ^를 사용) | Python (거듭제곱에 **를 사용) |
| y ~ I(x^2) + x | y ~ I(x**2) + x |
speed 와 dist
import pandas as pd
import seaborn as sns
sp = pd.read_excel('speed.xlsx')
sns.regplot(x='speed', y='dist', data=sp)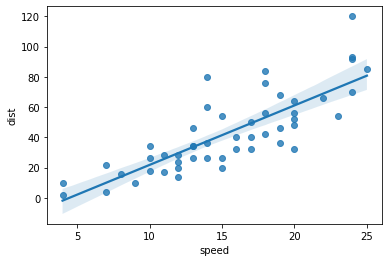
| 운동에너지가 속도**2에 비례한다는 것을 참고해서 I 함수로 속도 제곱값 적용 |
|
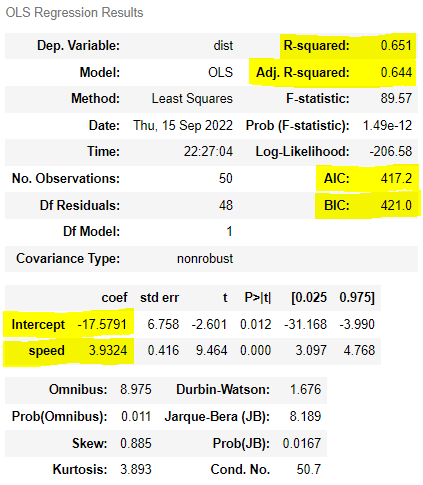
| from statsmodels.formula.api import ols ols('dist ~ speed', sp).fit().summary() |
from statsmodels.formula.api import ols ols('dist ~ I(speed**2) + speed', sp).fit().summary() # dist = 0.1 speed**2 + 0.9 speed + 2.4701 |
 |
 |
| dist = 3.9324 speed - 17.5791 | dist = 0.1 speed**2 + 0.9 speed + 2.4701 |
| > R²은 독립변수가 증가해서 증가하였고 AIC는 ▼ BIC는 ▲, 일부 면에서 좋은점이 있다. > 추가로 더 해보니 독립변수에 속도의 제곱만 넣은것이 수정된 R계수 증가, AIC와 BIC 모두 감소로 가장 좋은 모델이었다. |
|
절편이 없는 모형
절편이 없는 모형(b = 0)을 표시하기 위해서는 관계식에 0 +를 추가
y ~ 0 + x
# 절편을 없애고 싶을 때
from statsmodels.formula.api import ols
ols('dist ~0 + I(speed**2)', sp).fit().summary()
# dist = 0.1534 speed**2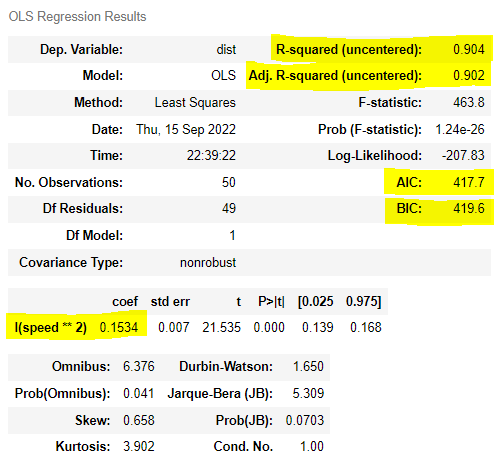
> 절편이 있을 때와 없을 때 R² 계산 방식이 다르다.
| · 절편이 있을 때 | · 절편이 없을 때 |
| R제곱 = 1 - 잔차분산 / (평균으로 예측할 때의 잔차분산) | R제곱 = 1 - 잔차분산 / (모든 값을 0으로 예 측할 때의 잔차분산) |
∴ 절편이 있을 때와 없을 때에는 R²과 수정된 R²으로 비교하면 안됨.
절편의 이동
절편 : x = 0 일 때의 예측치
• 절편을 x = 100일 때의 예측치로 바꾸려면 x에 일괄적으로 100을 빼면 됨
y ~ I(x – 100)
• 분석 자체에는 영향이 없으나 절편의 해석이 더 쉬워질 수 있음.
| ▶ 절편 이동 | |
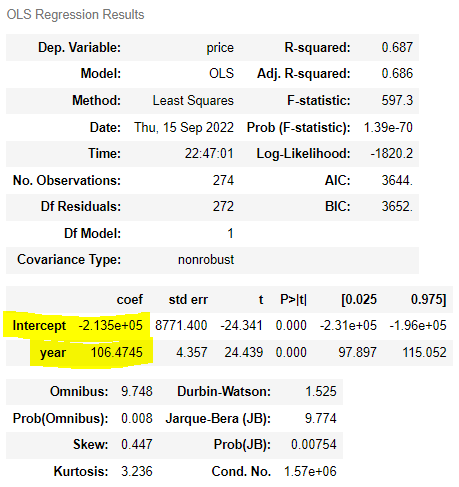
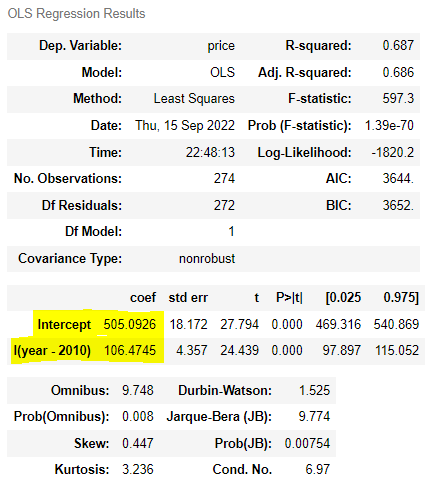
| ols('price ~ year', df).fit().summary() | ols('price ~ I(year-2010)', df).fit().summary() |
 |
 |
| price = 106.4745 x - 2.135 e+05 > 세상이 열릴 때쯤의 중고차의 가격은 사실 필요하지 않다. |
price = 106.4745 x + 505.0926 > 해석하기 좋은 임의의 날짜(2010년도)를 기준으로 잡을 때 |
∴ 기울기는 변하지 않는다. 다만, 목적에 따라 잡은 기준에서 절편 해석을 편하게 할 수 있다는 것.
독립변수 서열을 이용한 회귀분석
독립변수의 서열(등수)이 1 변할 때 종속변수의 변화
스피어만 상관계수와 비슷한 논리
| R | Python |
| y ~ rank(x) | y ~ x.rank() |
장점
- 표준화처럼 단위가 서로 다른 경우를 비교할 수 있다.
- 로그함수처럼 한쪽이 늘어진 데이터를 고르게 맞춰줄 수 있다.
단점
- 새로운 데이터는 기존 데이터의 등수에 맞춰서 등수를 산정해야 함.
- 예측을 할 때 새로 들어온 데이터가 기존의 관찰 범위를 넘어서면 예측을 못함.
(등수를 매겨놨기 때문에 등수에 있는 범위 밖에 데이터가 들어오면 예측을 못함)
import numpy as np
ols('price ~ year.rank() + mileage.rank()', df).fit().summary()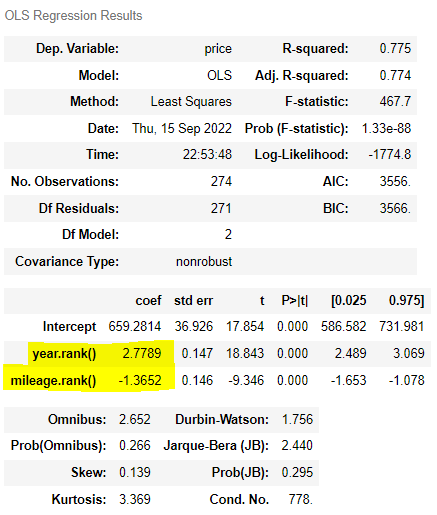
> 중고차 N대를 서열로 나열했을 때, year과 mileage의 순서에 따라 등수가 변할 때 coef만큼 가격이 변화한다.
독립변수 서열을 이용한 회귀분석 .rank() 의 단점
예시) 중고차(car.xlsx 데이터)
| train 데이터 | test 데이터 |
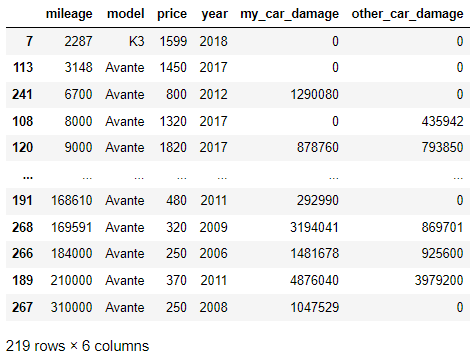
| from sklearn.model_selection import train_test_split train_df, test_df = train_test_split(df, test_size=0.2, random_state=42) train_df.sort_values('mileage') |
test_df.sort_values('mileage').head() test_df.sort_values('mileage').tail() |
 |
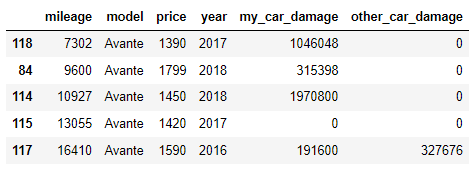 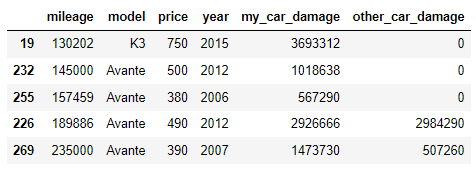 |
| > 새로운 데이터(위의 경우, test data)는 기존 데이터(train_data)의 등수에 맞춰서 등수를 산정해야 함. | |
'기초통계' 카테고리의 다른 글
| [실습] 회귀분석 : birthsmokers data (0) | 2022.09.10 |
|---|---|
| 로지스틱 회귀분석 (0) | 2022.09.06 |
| 다중회귀분석 : 단계적 회귀분석 (0) | 2022.09.06 |
| 다중회귀분석 : 교차검증 (0) | 2022.09.06 |
| 회귀분석 : 다중회귀분석 (0) | 2022.09.05 |