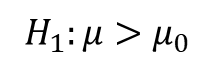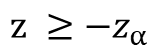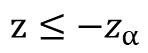📌 본 포스팅은 통계교육원(https://sti.kostat.go.kr/)
이러닝 교육과정 '통계학의 이해(2023)' 강의에 대한 복습 기록입니다.
모든 내용은 강의 교안을 기준으로 작성했으며 원본 자료는 하단 통계교육원 - 교육과정 - 이러닝 - '통계학의 이해' 교육 수강을 통해 무료로 열람 가능하고 교육자료는 저작권자의 동의 없이 무단 복제 및 배포할 수 없습니다.
🎯 모평균에 대한 가설검정
💡 모집단의 분포가 정규분포일 때
모평균에 관한 추정을 할 때 표본평균을 이용하는 것은 매우 보편적이다.
마찬가지로 모평균에 대한 가설검정을 할 때도 표본평균을 이용하는 것이 합리적이고,
표본평균의 분포인 표본분포를 이용하여 모평균에 대한 가설검정을 실시할 수 있다.
모집단의 분포가 정규분포일 때
예제로 모평균의 가설검정 알아보기

학생들 평균 IQ가 100보다 작은지가 궁금하기 때문에 단측 가설을 세울 수 있다.
- 귀무가설(H 。) : μ = 100
- 대립가설(H₁ ) : μ < 100
문제에서 IQ가 정규분포를 따르므로, 표본평균의 분포도 정규분포를 따른다.
귀무가설이 참이라고 가정하면 → 표본평균의 분포는 평균이 100이고, 분산은 144/9인 정규분포를 따른다.

따라서 표준화된 표본평균 Z는 아래와 같이 표준정규분포를 따른다.
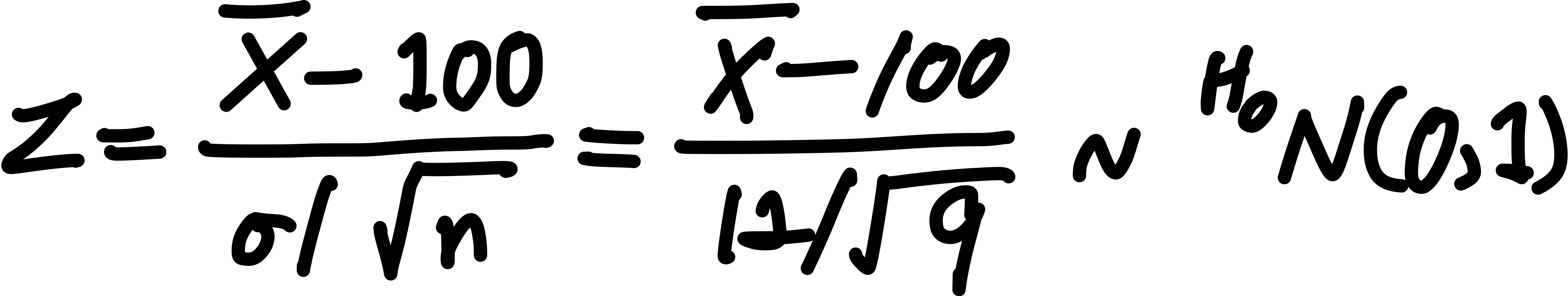
즉, 귀무가설이 '참'이라고 가정하면(실제 학생IQ의 평균이 100이라고 가정)하면
n=9개의 표본으로부터 계산된 z값은 0 근처에서 나올 가능성이 높고
0과 멀어진 값이 나올 가능성은 점점 작아진다는 것을 의미한다.
다시 말해, 표본으로부터 계산한 값이 0에서 멀어질수록
귀무가설을 기각하고, 대립가설을 지지하는 근거가 되는 것.
그렇다면 어떤 결과가 나왔을 때 귀무가설을 기각하고 대립가설을 지지하나? 🤔
둘중 하나의 가설을 선택하기 위해서는 유의수준(제1종의 오류의 최대 허용확률)이 필요하다.
예제에서는 유의수준 5%에서 검정하라고 했으므로
Z값이 나올 가능성이 5%보다 작다면 귀무가설을 기각한다.
여기서 Z값을 기준으로 검정을 시행하기 때문에 통계량 Z를 검정통계량이라 한다.
📌 표준정규분포 확률에 의해 Z값이

보다 작을 확률은 정확히 0.05이다.
따라서 표본으로부터 계산한 z값이 -1.645보다 작으면, 귀무가설을 기각할 수 있다.
위 예제에서 표본으로부터 Z값을 계산해보면

즉

보다 작으므로 귀무가설을 기각할 수 있다.
모평균에 대한 가설검정
모집단이 정규분포를 따르고 분산이 알려져 있을 때

다음과 같이 귀무가설, 대립가설이 주어지면

모평균에 대한 가설검정은 아래와 같이 검정통계량을 고려할 수 있고
이 검정통계량은 귀무가설이 참이라고 가정하면, 표준정규분포를 따른다.

주어진 표본으로부터 검정통계량 값을 Z라하면
주어진 유의수준 α에 대해, z < -z(유의수준)보다 작으면 귀무가설을 기각할 수 있다.
여기에서, z < -z(유의수준)을 유의수준 α에서의 기각역이라고 한다.
✔ 만약,
대립가설이 아래와 같이 반대방향으로 주어지면, 기각역도 반대방향으로 z > z(유의수준)이다.

대립가설이 양측방향으로 주어지면, 대립가설은 다음과 같이 설정해야 한다.
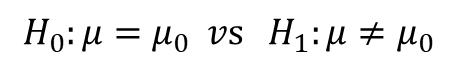
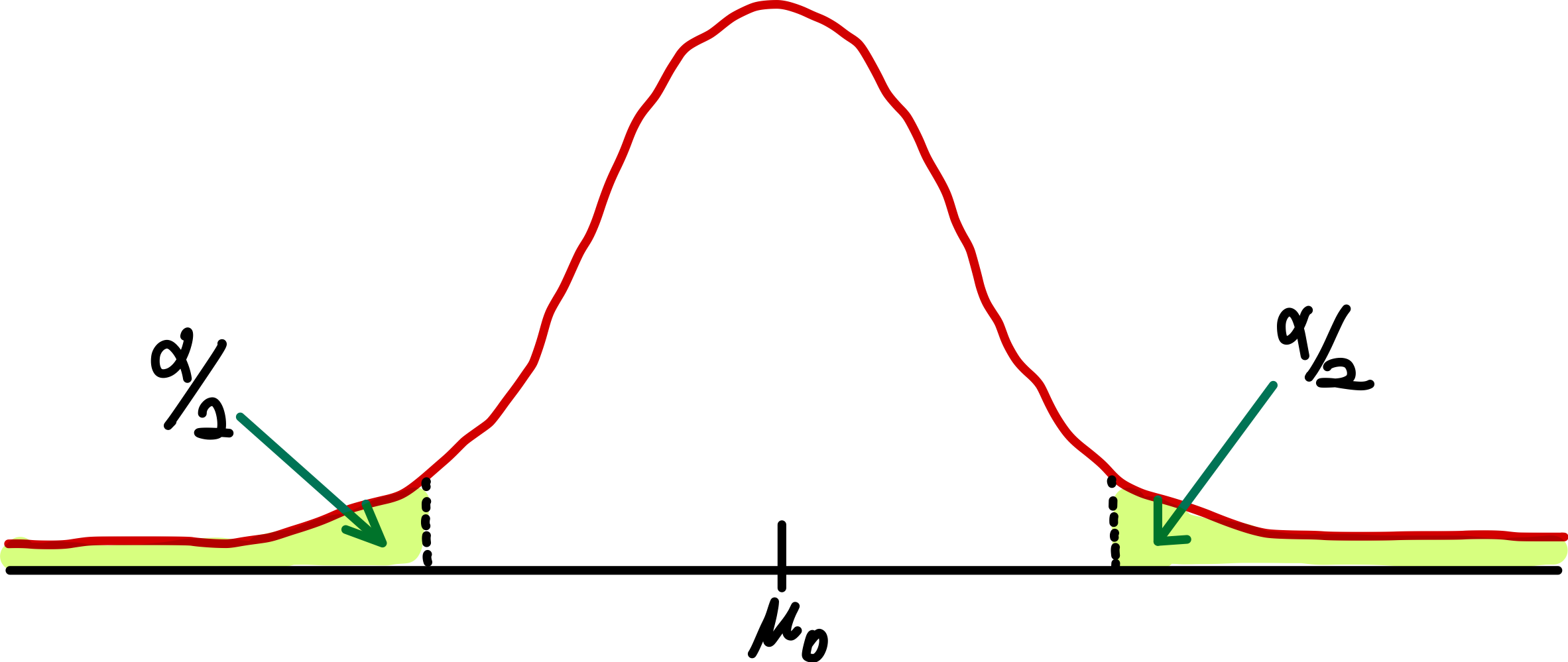
검정통계량 값 z가 큰 것이나, 작은 것 모두 바람직하기 않기 때문에 양쪽 방향을 모두 고려해서 기각역을 설정할 수 있다. 양쪽 끝에 배분하는 방법은 여러가지가 있으나, 아래 그림과 같이 똑같이 배분하는 것이 가장 좋은 것으로 알려져 있다.
따라서 이 경우, 기각역은 z < -z(유의수준) 이거나 z > z(유의수준) 이다. 즉 |z| > z (유의수준)/2 이다.
정리하기
모평균에 대한 검정을 할 때 대립가설 형태로는 다음과 같이 세 유형의 가설이 나온다.
✔ 모평균 μ에 대한 검정에 사용할 검정통계량

✔ 세가지 대립가설에 대해 귀무가설(H 。) : μ = μ。을 검정할 기각역은 아래 표와 같다.
| 대립가설 | 유의수준 α에서의 기각역 |
'기초통계' 카테고리의 다른 글
| [통계학의 이해] 18. 모평균에 대한 가설검정3 - 모집단이 정규분포가 아닌 경우 #중심극한정리 - 예제 (1) | 2023.10.04 |
|---|---|
| [통계학의 이해] 18. 모평균에 대한 가설검정2 : t-검정 (0) | 2023.10.04 |
| [통계학의 이해] 17. 가설검정의 원리 (0) | 2023.09.30 |
| [통계학의 이해] 16. 신뢰구간의 이해 -2 (0) | 2023.09.26 |
| [통계학의 이해] 15. 신뢰구간의 이해 -1 (0) | 2023.09.25 |