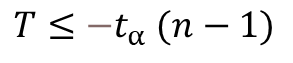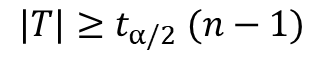📌 본 포스팅은 통계교육원(https://sti.kostat.go.kr/)
이러닝 교육과정 '통계학의 이해(2023)' 강의에 대한 복습 기록입니다.
모든 내용은 강의 교안을 기준으로 작성했으며 원본 자료는 하단 통계교육원 - 교육과정 - 이러닝 - '통계학의 이해' 교육 수강을 통해 무료로 열람 가능하고 교육자료는 저작권자의 동의 없이 무단 복제 및 배포할 수 없습니다.
🎯 모평균에 대한 가설검정2
💡 모집단의 분포가 정규분포지만 모분산을 모를 때
모집단의 분포가 정규분포지만 모분산을 모를 때
모평균의 가설검정 알아보기
모평균에 대한 가설검정에 있어서 실제로는 모분산을 모르는 경우가 대부분이다.
검정통계량 Z의 분모가 σ가 포함되어 있기 때문에 σ를 알고 있다면 검정통계량 Z를 사용할 수 있다.
그러나 σ를 모를 때에는 그의 추정량 S 를 사용하여 검정통계량을 사용한다.
· 추정량 S
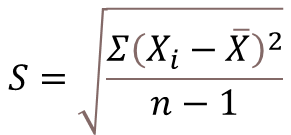
· 검정통계량 T

모집단이 정규분포를 따르고, 귀무가설이 '참'이라고 가정하면
위 검정통계량 T는 자유도가 (n-1)인 t-분포를 따른다.
따라서 비슷하게 대립가설에 따른 기각역을 아래와 같이 구할 수 있다.
| 대립가설 | 유의수준 α에서의 기각역 |
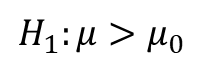 |
|
 |
|
 |

✔ 1번 풀이

✔ 2번 풀이
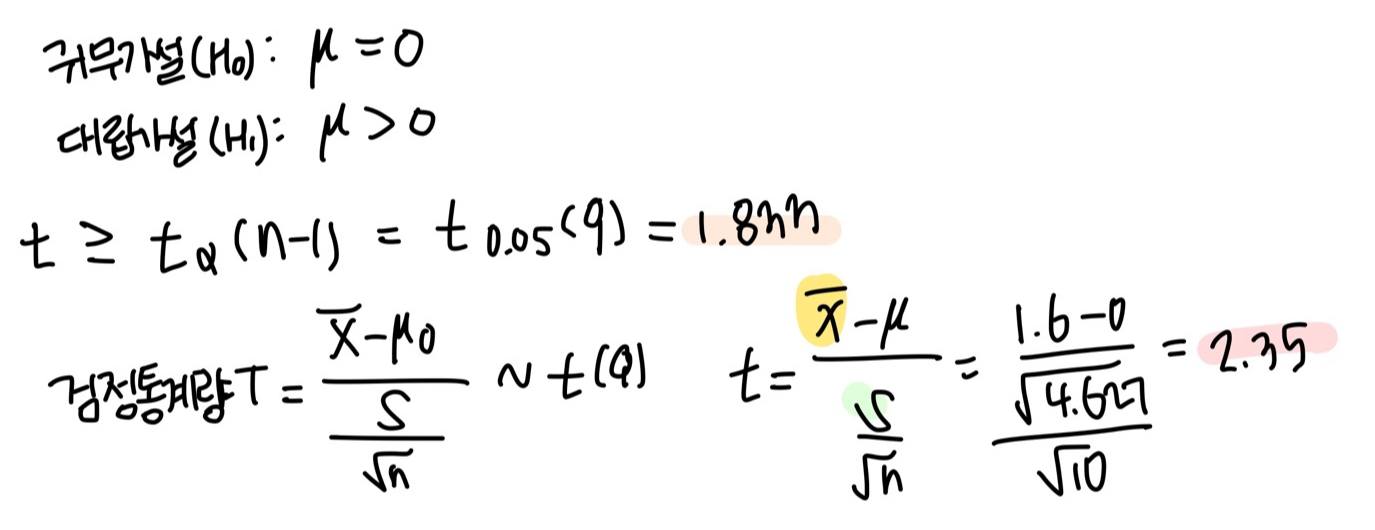
α = 0.05 에서 결정기준은 1.833 (t분포표 참고*)
검정통계량 관측값이 2.35로 기각역에 속하기 때문에 유의수준 5%에서 귀무가설을 기각할 수 있다.
즉, 유의수준 5%에서 다이어트 식품은 효과가 있다고 할 수 있다.
요약
모집단이 정규분포인 경우에는 표본의 크기와 상관없이 검정통계량인 표본평균의 분포가
- 모분산을 알 때는 정규분포,
- 모분산을 모를 때에는 t-분포를 따른다.
는 사실을 이용해서 모평균 μ에 대한 가설 검정을 할 수 있다.
'기초통계' 카테고리의 다른 글
| [통계학의 이해] 19. 유의확률(p-value)과 모비율에 대한 검정 - 유의확률(p-value) (1) | 2023.10.18 |
|---|---|
| [통계학의 이해] 18. 모평균에 대한 가설검정3 - 모집단이 정규분포가 아닌 경우 #중심극한정리 - 예제 (1) | 2023.10.04 |
| [통계학의 이해] 18. 모평균에 대한 가설검정 - 예제 풀이 (0) | 2023.09.30 |
| [통계학의 이해] 17. 가설검정의 원리 (0) | 2023.09.30 |
| [통계학의 이해] 16. 신뢰구간의 이해 -2 (0) | 2023.09.26 |