📌 본 포스팅은 통계교육원(https://sti.kostat.go.kr/)
이러닝 교육과정 '통계학의 이해(2023)' 강의에 대한 복습 기록입니다.
모든 내용은 강의 교안을 기준으로 작성했으며 원본 자료는 하단 통계교육원 - 교육과정 - 이러닝 - '통계학의 이해' 교육 수강을 통해 무료로 열람 가능하고 교육자료는 저작권자의 동의 없이 무단 복제 및 배포할 수 없습니다.
🎯 유의확률(p-value) 개념 알기
모비율에 대한 가설검정
💡 유의성 검정, 유의확률, 모비율, 중심극한정리, 신뢰구간
이전 차시까지는 검정통계량을 이용해서 검정을 실시했다.
보통 유의수준 5%에서 검정기준(기각역)과 검정통계량을 비교.
유의수준은 제1종오류의 최대허용한계이기 때문에 상황에 따라 다르게 책정할 수 있다.
이런 상황에서 검정규칙을 일일히 새로 구하는 것은 매우 번거로울 수 있다.
따라서 다른 접근 방법인 유의확률(p-value)를 이용한 방법을 살펴보려고 한다.


관측값 102가 나올 가능성이 귀무가설이 참일 때보다, 대립가설이 참일 때 더 높다면
→ 관측값(102)는 귀무가설이 거짓이고, 대립가설이 참이라는 증거가 될 수 있다.
→ 귀무가설이 참일 때, 관측값이 102보다 작으면 작을수록 귀무가설이 참이 아니라는 더 확실한 증거가 된다.
이렇게 표본으로부터 얻은 값(증거)의 확실한 정도를 확률로 표현한 것이
바로 '유의확률(significant probability)' 또는 p-값(p-value)라 한다.
# 유의확률(p-value)
귀무가설이 참일 때,
검정통계량이 표본에서 계산된 값과 같거나 그 값보다 대립가설 방향으로 더 극단적인 값을 가질 확률
유의확률이 작을수록 표본에서 얻은 결과가 '귀무가설이 사실이 아니다'의 확실한 증거가 된다.
유의확률은 귀무가설이 '참'이라고 했을 때 현재 가지고 있는 자료가 나올 확률.
'유의확률이 작다'
→ 귀무가설이 참이라고 하면 귀무가설이 나올 가능성이 매우 적기 때문에 귀무가설을 기각하고 대립가설을 지지하는 것.
🕵️♂️ 수식으로 이해하기
✔ 모평균의 가설검정에 대한 검정통계량과 분포

주어진 자료에서 계산된 검정통계량 z
유의확률은 귀무가설이 참일 때, 검정통계량이 주어진 자료로 계산된 z값보다 극단적인 확률
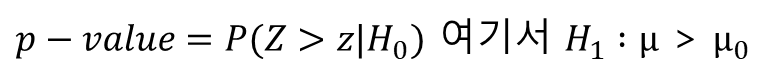

가설검정에서 표본의 관측치를 바탕으로 얻은 유의확률이 주어진 유의수준 α와 같거나 작으면 귀무가설을 기각한다.
유의확률은 검정통계량의 분포를 이용해서 구한다.
유의확률이 지정된 유의수준( α ) 이하로 나타남.
→ 유의수준 α에서 유의하다 → 귀무가설에 대한 반증의 강도가 지정된 수준보다 강하다.
일반적으로 유의수준 α 는 0.1, 0.05, 0.01을 주로 사용한다.
요약
📌 모집단이 정규분포를 따르고, 모분산을 알고있을 때
# 검정통계량

< 대립가설 형태에 따른 기각역과 유의확률 >

✔ 유의확률 p값이 유의수준 α보다 작거나
관측값 z가 기각역에 포함되면, 귀무가설 H。를 기각한다. (즉, 대립가설 H₁를 채택)
'기초통계' 카테고리의 다른 글
| [통계학의 이해] 19. 유의확률(p-value)과 모비율에 대한 검정 - 모비율에 대한 가설검정 (0) | 2023.10.18 |
|---|---|
| [통계학의 이해] 19. 유의확률(p-value)과 모비율에 대한 검정 (예제) (1) | 2023.10.18 |
| [통계학의 이해] 18. 모평균에 대한 가설검정3 - 모집단이 정규분포가 아닌 경우 #중심극한정리 - 예제 (1) | 2023.10.04 |
| [통계학의 이해] 18. 모평균에 대한 가설검정2 : t-검정 (0) | 2023.10.04 |
| [통계학의 이해] 18. 모평균에 대한 가설검정 - 예제 풀이 (0) | 2023.09.30 |